Question

Rate constant k of a reaction varies with the temperature according to the equation $\log k = \log A - \dfrac{{{E_a}}}{{2.303R}}\left( {\dfrac{1}{T}} \right)$ where ${E_a}$ is the activation energy. When a graph is plotted for $\log k$ versus $\dfrac{1}{T}$, a straight line with a slope $- 4250\;K$ is obtained. Calculate ‘${E_a}$’ for the reaction. $\left( {R = 8.314\;J{K^{ - 1}}mo{l^{ - 1}}} \right)$

Answer 1

In chemistry, the speed of a chemical reaction is determined by its reaction rate. It is often expressed in terms of either concentration of products formed during a chemical reaction or in terms of concentration of reactants consumed in the reaction. The proportionality constant which is used to express rate of reactions in terms of concentration of reacting substances is known as rate constant.

Complete answer:
Arrhenius equation: This equation is used to express rate constant in terms of temperature of reaction and its activation energy. It can be used to determine how the rate of a chemical reaction varies with an increase in temperature. The equation is expressed as follows:
$k = A{e^{\left( {\dfrac{{ - {E_a}}}{{RT}}} \right)}}\;\;\; - (1)$
Where, k is the rate constant, A is the frequency or pre-exponential factor, ${E_a}$ is the activation energy i.e., the minimum energy required to proceed the reaction, R is the universal gas constant and T is the temperature of the system.
Arrhenius equation can be used in determining the activation energy as follows:
Taking log on both sides for equation (1) and separating the pre-exponential and exponential terms, the Arrhenius equation will be expressed as follows:
$\ln k = \ln \left[ {A{e^{\left( {\dfrac{{ - {E_a}}}{{RT}}} \right)}}} \right]$
$\Rightarrow \ln k = \ln A + \ln {e^{\left( {\dfrac{{ - {E_a}}}{{RT}}} \right)}}\;\;\;\;\left[ {\because \ln ab = \ln a + \ln b} \right]$
$\Rightarrow \ln k = \ln A - \dfrac{{{E_a}}}{R}\left( {\dfrac{1}{T}} \right)\;\;\;\;\left[ {\because \ln {e^a} = a} \right]$
Converting natural logarithm into log base 10:
$\Rightarrow 2.303\log k = 2.303\log A - \dfrac{{{E_a}}}{R}\left( {\dfrac{1}{T}} \right)\;\;\;\;\left[ {\because \ln a = 2.303\log a} \right]$
On simplifying the expression:
$\Rightarrow \log k = \log A - \dfrac{{{E_a}}}{{2.303R}}\left( {\dfrac{1}{T}} \right)$
It represents an equation of type $y = mx + c$ which is a straight-line equation and its slope is negative. Graphically, it is represented as follows:

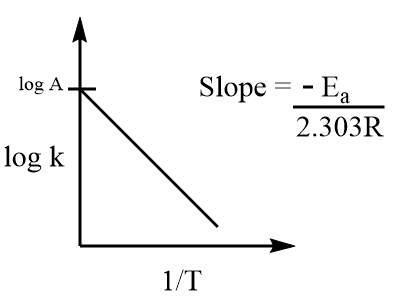
Where, $\log A$ is the intercept and $- \dfrac{{{E_a}}}{{2.303R}}$ is the slope of the curve.
Now, according to the question, the slope of the curve is $- 4250\;K$. Substituting the value in the expression of slope, the value of activation energy will be as follows:
$- \dfrac{{{E_a}}}{{2.303R}} = - 4250$
$\Rightarrow {E_a} = 4250 \times 2.303R$
Substituting value of R as given in the question:
$\Rightarrow {E_a} = 4250 \times 2.303 \times 8.314$
$\Rightarrow {E_a} = 81375.4Jmo{l^{ - 1}}$
$\Rightarrow {E_a} = 81.38\;kJmo{l^{ - 1}}$
Hence, the activation energy for the given reaction condition is $81.38\;kJmo{l^{ - 1}}$.

Note:
It is important to note that the term ${e^{\dfrac{{ - {E_a}}}{{RT}}}}$ represents the fraction of collisions that a molecule may experience and it must have a sufficient energy to overcome the activation barrier. Moreover, from the graph it is clearly observed that on increasing the value of temperature, the value of the exponential part of the equation becomes less negative, therefore the rate constant and the rate of the reaction increases.