Question
Question: Rate constant k of a reaction varies with temperature according to the equation \[{\text{log}}\,{\te...
Rate constant k of a reaction varies with temperature according to the equation logk = constant - 2.303Ea \timesT1 where Ea is the energy of activation for the reaction. When a graph is plotted for logk vs T1 a straight line with a slope −6670K is obtained. The activation energy for this reaction will be: (R=8.314JK−1mol−1)
A.122.65kJmol−1
B.127.71kJmol−1
C.142.34kJmol−1
D.150.00kJmol−1
Solution
The minimum amount of extra energy required by a reacting molecule to get converted into product is called the activation energy. In the presence of a catalyst, the activation energy decreases a bit. The activation energy can also be described as the minimum amount of energy needed to activate molecules or atoms so that they can undergo a chemical reaction. Activation energy is denoted by Ea . It is usually measured in joules (J) and or kJmol−1 or kcalmol−1 .
Complete step-by-step answer: The given Arrhenius equation;
logk = constant - 2.303Ea \timesT1
Let’s write constant as log A ;
Now, we know that the plotted graph is a straight line; which means,
y=c+mx
Therefore, y will be logk, c will be constanti.e., log A and the remaining term mx will be - 2.303Ea \timesT1 where xwill be [T1].
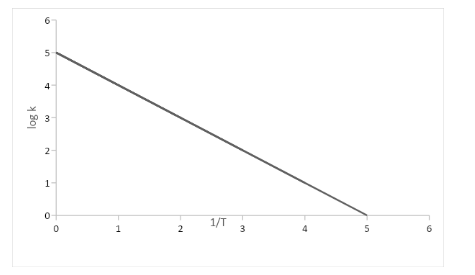
In this graph, we are able to observe that [T1] which is on x axis and logk values on y axis.
Where the given intercept value which will be our term c .
=−2.303REa
Now, we need to find Ea, i.e., activation energy.
So, let’s write the reaction in which the values are given;
slope =−6670K
let’s observe the equation, we need to find activation and we have the value of slope.
So,
Slope of the line =−2.303REa
Ea=−2.303R×slopeoftheline
slope=−6670K
Ea=−2.303R×8.314×(−6670)
=127711.4
=127.71KJmol−1
So, the activation energy is 127.71KJmol−1
Therefore, the correct answer is option B.127.71kJmol−1
Note: A catalyst is a chemical substance that either increases or decreases the rate of a chemical reaction. In the case of activation energy, a catalyst lowers it. Since, the energies of the reactants will remain the same. A catalyst only changes the activation energy. There can be positive catalysts or else negative catalysts too.
