Question

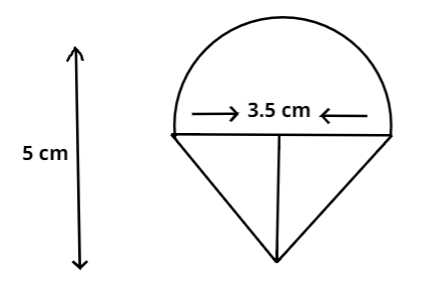
Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with crayons. The top is shaped like a cone surmounted by a hemisphere. The entire top is $5cm$ in height and the diameter of the top is $3.5cm$.Find the area he has to colour. (Take $\pi = \dfrac{{22}}{7}$)

A. $37.2c{m^{^2}}$
B. $30.2c{m^{^2}}$
C. $49.2c{m^{^2}}$
D. $39.6c{m^{^2}}$

Answer 1

Hint: Here, we will find the area of the top by calculating the radius and Slant height of the conical part since the top is shaped like a cone surmounted by a hemisphere.Here height of cone can be calculated by difference of total height of top and radius of hemisphere.Then find the slant height and total surface area of both cone and hemisphere using formulas.

Complete step-by-step answer:
We have been given with the diameter of the lattu, using this we can find the radius,
Radius of the hemispherical portion of the lattu = $\dfrac{{3.5}}{2} = \dfrac{7}{4}cm$
Since the top is shaped like a cone surmounted by a hemisphere, therefore the radius of the lattu will also be the radius of cone, therefore,
Radius of the conical portion, $r = \dfrac{{3.5}}{2} = \dfrac{7}{4}cm$
Height of the conical portion=Total height of top -radius of sphere ,we get
$h = \left( {5 - \dfrac{{3.5}}{2}} \right) = \dfrac{{13}}{4}cm$
Using the formula of slant height we will calculate the slant height by assigning the above value, therefore,
Slant height of the conical part, $l = \sqrt {{r^2} + {h^2}}$
$l = \sqrt {{{\left( {\dfrac{7}{4}} \right)}^2} + {{\left( {\dfrac{{13}}{4}} \right)}^2}} = \sqrt {\dfrac{{218}}{4}} = 3.69cm \approx 3.7cm$
Total surface area of the top=Surface area of hemisphere + Surface area cone
We know surface area of hemisphere =$2\pi {r^2}$ and Surface area of cone =$\pi rl$ then substituting the values we get,
$2\pi {r^2}$ + $\pi rl$ = $\pi r\left( {2r + l} \right)$ = $\dfrac{{22}}{7} \times \dfrac{7}{4}\left( {2 \times \dfrac{7}{4} + 3.7} \right) = 39.6c{m^2}$
The area he has to colour the top is $39.6c{m^2}$
Therefore, Option D is correct.

Note: While solving these problems based on the cone shapes, make sure to know the difference between height (h) and slant height (l).One should remember calculating the height of the cone,it is the difference of total height of top and radius of hemisphere. Students should remember the important formulas of total surface area of cone and hemisphere.