Question

Ranjini makes arrangements for a candle light dinner and tops it with a dessert of gelatin filled blueberries. If a blubbery that appears at an angle of $45^\circ$ to the normal in air is really located at $30^\circ$ to the normal in gelatin, what is the index of refraction of gelatin?

Answer 1

Gelatin is a transparent medium for light to pass. It causes the light to bend/ refract. Keep in mind that, when a ray of light passes from an optically rarer to an optically denser medium, it bends towards the normal after refraction and vice-versa.

Complete step by step answer:
Let’s first discuss the phenomenon of refraction of light first. When studying geometric optics, we will hear a lot about refraction
The phenomenon of change of the path of light at the medium of separation as it goes from one medium to another is called refraction.
When a ray of light passes from a denser medium to a rarer medium, the ray bends away from normal after establishment of refraction.
There are certain laws assigned to refraction. They are as follows:
1. Whenever light travels from one medium to another, the frequency of light does not change, however the velocity and its wavelength change.
2. The incident ray, refracted ray, and normal to the interface at the point of incidence all lie in the same plane.
3. For two particular media and for a given colour of light, the ratio of sine angle of incidence to the sine angle of refraction is a constant. This is known as Snell’s law.
4. If $i$ is the angle of incidence and $r$ is the angle of refraction,
a) $\dfrac{{\sin i}}{{\sin r}} = CONSTANT$
b) This constant is known as refractive index of the second medium with respect to the first medium.
c) The refractive index of the second medium with respect to first medium is represented by $^1{\mu _2}.$
That is, $\dfrac{{\sin i}}{{\sin r}}{ = ^1}{\mu _2} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$ ………. (1)

Now, let’s look at the given problem.

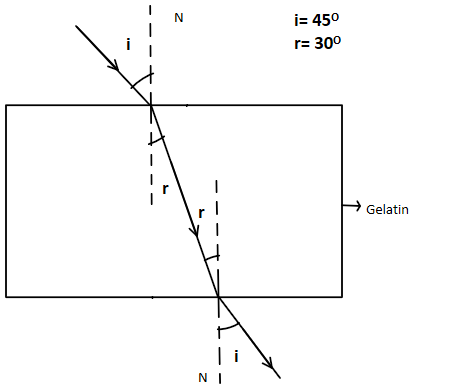
From the above diagram, we can discuss the angle of incidence and angle of refraction fro the blue berry at the normal N.
The angle of incidence that is the angle of blueberry to the normal as viewed from air is $i = 45^\circ$ and the angle of refraction that is the actual angle to the normal at which the blueberry is located, is$r = 30^\circ$.
By Snell’s law of refractive index,
$^1{\mu _2} = \dfrac{{\sin i}}{{\sin r}} = \dfrac{{\sin 45^\circ }}{{\sin 30^\circ }}$
${ \Rightarrow ^1}{\mu _2} = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{\dfrac{1}{2}}} = \dfrac{2}{{\sqrt 2 }}$
${ \Rightarrow ^1}{\mu _2} = 1.41$

So the refractive index for the gelatin will be $1.41$.

Note: Refractive index is a measure of strength of refraction of the medium. The more is the refractive index, the more a ray of light will bend away from the normal. Sometimes the examiner might ask about the units or dimensions of the physical quantity refractive index. However it does not possess any unit or dimension for it is a pure ratio between sine angles of incidence and refraction.