Question
Question: Range of f(x) = [1 + sinx] + \(\left[ 2 + \sin \frac { x } { 2 } \right]\)+ \(\left[ 3 + \sin \frac...
Range of f(x) = [1 + sinx] + [2+sin2x]+ [3+sin3x] + ..... + [x+sinnx]∀ x ∈ [0, π], where [.] denotes the greatest integer function, is
A
{2n2+n−2,2n(n+1)}
B

C
{2n2+n−2,2n(n+1),2n2+n+2}
D

Answer

Explanation
Solution
f(x)=2n(n+1)+[sinx]+[sin2x] +… +[sinnx]
Since x ∈ [0, π] . Thus range is
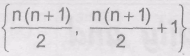
⇒ ((52)x+(53)x+(54)x−1) = 0
Clearly g(x)=(52)x+(53)x+(54)x−1 is a
decreasing function and Limx→∞g(x) = −1, Limx→−∞ g(x) = ∞ also g(0) = 1. Thus f(x) = 0 has exactly one root.
