Question

Raindrops fall vertically at speed of $20m{{s}^{-1}}$ .at what angle do they fall on the windscreen of a car moving with velocity of $15m{{s}^{-1}}$ .If the wind screen velocity inclined at an angle of ${{23}^{0}}$ to the vertical? $({{\cot }^{-1}}\dfrac{4}{3}={{37}^{0}})$
A) ${{60}^{0}}$
B) ${{30}^{0}}$
C) ${{90}^{0}}$
D) ${{45}^{0}}$

Answer 1

Speed is defined as the distance covered per unit time and speed is a scalar quantity. SI unit of speed is $m{{s}^{-1}}$ . Displacement is defined as the process in which objects' positions are changed and in displacement the initial position of objects are changed. Displacement is also defined as change in initial position of objects to the final position and displacement is denoted as S.

Complete step by step solution:
Velocity is defined as the rate of change of displacement with respect to time and in kinematics velocity is a fundamental concept.SI unit of velocity is $m{{s}^{-1}}$ Velocity tracking is the measure of velocity.
Velocity (v) =$\dfrac{\Delta S}{\Delta t}$
The dimensional formula of velocity is ${{M}^{0}}{{L}^{1}}{{T}^{-1}}$.
From the data
Velocity of rain( ${{v}_{r}}$ )=-20j
Velocity of car (${{v}_{c}}$ )=15i

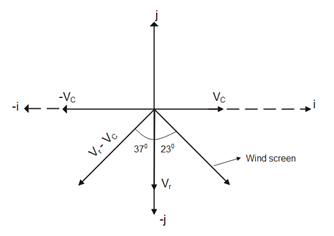
Therefore the velocity of rain with respect to car ($v$ ) = ${{v}_{r}}-{{v}_{c}}$
$v=-20j-15i$
Angle made by rain (${{\theta }_{r}}$ wrt wind screen is given as:
${{\theta }_{r}}=\theta +{{23}^{0}}$
From the data the value of $\theta ={{37}^{0}}$
After substituting these value in the above equation
We get ${{\theta }_{r}}={{60}^{0}}$
So the rain will fall at ${{60}^{0}}$ on the wind screen
The correct option is A.

Note: When you are moving in a car the raindrop appears to the moving towards you, but that is actually because you are moving towards you, but that is actually because you are moving towards it, in the same way that trees appear to be moving in the opposite direction to you if you look out of the side window.