Solveeit Logo
Login

Question

Question: Raindrops are falling with a velocity \(10\sqrt 2m/s\) making an angle \(45^{\circ}\) with the verti...

Raindrops are falling with a velocity 102m/s10\sqrt 2m/s making an angle 45∘45^{\circ} with the vertical. The drops appear to be falling vertically to a man running with constant velocity. The velocity of rain drops changes such that the rain drops now appear to be falling vertically with 3\sqrt 3 times the velocity it appeared earlier to the same person running with the same velocity. The magnitude of man with respect to ground is :

& A.10\sqrt{2}m/s \\\ & B.10\sqrt{3}m/s \\\ & C.10m/s \\\ & D.20m/s \\\ \end{aligned}$$
Explanation

Solution

We have the velocity of the rain droplets. Given that the man is moving with some velocity with respect to the rain drops. To find the velocity of the man, we need to resolve the components of velocity of the rain droplets.

Formula used: vm=vrcosθv_{m}=v_{r}cos\theta

Complete step by step answer:
Consider the diagram shown below, let CC be the rain cloud and let MM be the man.
Given that the velocity of the raid drop is vr=102m/sv_{r}=10\sqrt2m/smaking an angle 45∘45^{\circ} with the vertical.

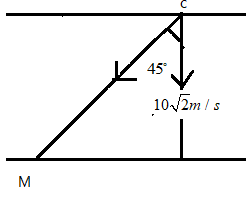
We can say that the velocity of the man with respect to the ground , here is the component of the velocity of the rain, it is given as vm=vrcos45=10212=10m/sv_{m}=v_{r}cos45=10\sqrt2\dfrac{1}{\sqrt2}=10m/s
Since the person runs with the same velocity, even if the velocity of the rain increases. The velocity vmv_{m} remains unchanged. Thus the final velocity of the man is given as vm=10m/sv_{m}=10m/s

So, the correct answer is “Option C”.

Additional Information: Since velocity is a vector we know that it has both direction and magnitude. Here since it makes some angle with the vertical it can be resolved into two perpendicular components, namely the vertical component and the horizontal component. From basic trigonometry, we can find the magnitude of the vector or the angle it makes. Using the phasor diagram we can find the direction or the orientation of the vector.

Note: This sum may seem very hard at first glance, but if one draws the diagram and labels the diagram correctly, it is easy to solve the question. The sum is simplified as the person is moving with the same velocity.