Question

Rain pouring down at an angle of $\alpha$ with vertical has a speed of $10m{s^{ - 1}}$ . A girl runs against the rain with a speed of $8m{s^{ - 1}}$ and sees that the rain makes an angle $\beta$ with the vertical. The relation between $\alpha$ and $\beta$ is:
[A] $\tan \alpha = \dfrac{{8 + 10\sin \beta }}{{10\cos \beta }}$
[B] $\tan \beta = \dfrac{{8 + 10\sin \alpha }}{{10\cos \alpha }}$
[C] $\tan \alpha = \tan \beta$
[D] $\tan \alpha = \cot \beta$

Answer 1

In order to solve this question we need to understand relative motion. So when the two bodies are moving with respect to one another then the motion of the second body viewed or observed from the first body is termed as relative motion. Also in this question we are going to use the triangle law of vector addition, which states that if two vectors are represented as two sides of a triangle then the third line or vector joining one’s tail and another’s head is termed as the sum of two vectors.

Complete step by step answer:
Let the rain fall down at a speed of ${\vec V_R} = 10m{\sec ^{ - 1}}$ in the direction as shown in figure.

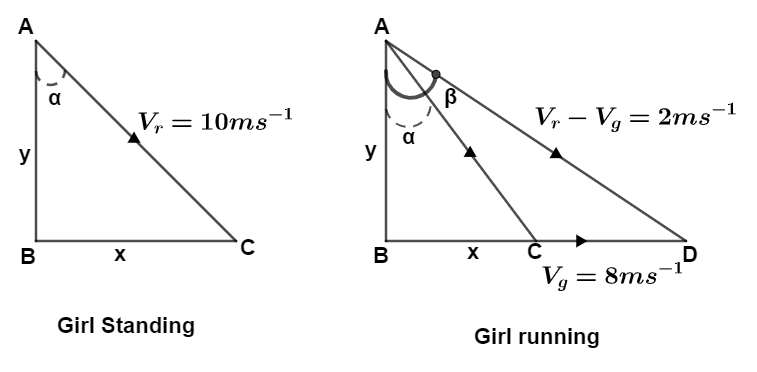
So when a girl is standing still, rain makes an angle of $\alpha$ with vertical as per given in problem.
Let the horizontal distance be, $x$ and vertical distance be $y$
So by using trigonometry in triangle $ABC$ we get, $\sin \alpha = \dfrac{x}{{{V_R}}}$
So horizontal length BC is, $x = {V_R}\sin \alpha$
Putting value we get, $x = 10\sin \alpha$
Similarly, by using trigonometry in triangle $ABC$ we get, $\cos \alpha = \dfrac{y}{{{V_R}}}$
So vertical length AB is, $y = {V_R}\cos \alpha$
Putting value we get, $y = 10\cos \alpha$
Now let the girl start running in opposite direction with the given speed, so the vector $C\vec D$ is, $C\vec D = - {\vec V_g}$
According to question, $C\vec D = - 8m{s^{ - 1}}$
So the length CD would be, $\left| {C\vec D} \right| = 8$
Now let the angle made by relative velocity ${\vec V_{Rg}}$ be, $\beta$
Also ${\vec V_{Rg}} = {\vec V_R} - {\vec V_g}$ (From triangle law of vector addition)
So using trigonometry in triangle ABD we get, $\tan \beta = \dfrac{{BD}}{{AB}}$
$\tan \beta = \dfrac{{BC + CD}}{{AB}}$
Putting values of length we get, $\tan \beta = \dfrac{{x + 8}}{y}$
Putting value of “x” and “y” we get, $\tan \beta = \dfrac{{10\sin \alpha + 8}}{{10\cos \alpha }}$
So the correct option is, [B] $\tan \beta = \dfrac{{8 + 10\sin \alpha }}{{10\cos \alpha }}$ .

Note:
It should be remembered that only those physical quantities can be regarded as vectors if they have both magnitude and direction. Also, they must satisfy, triangle law of vector addition. Triangle law of vector addition must be satisfied, it is a necessary condition, for example electric current has both magnitude and direction but since it does not satisfy triangle law of vector addition, it is not a vector.