Question

Rain is falling with the speed of $25\sqrt 3 m/s$ vertically. The wind blows west to east at a speed of $25m/s$ . Find the velocity of rain as experienced by a person standing on ground:
A.$50m/s$
B.$100m/s$
C.$0m/s$
D.$90m/s$

Answer 1

The velocity of rain as experienced by a person is the resultant of the speed of the rain falling vertically downwards and the speed of the wind taking the ground as a reference frame.

Complete answer:
Rain is falling vertically downwards with the speed (${v _r}$) of $25\sqrt 3 m/s$ . So $\overrightarrow {{v_r}} = 25\sqrt 3 j$ $m/s$ .
The wind is blowing from west to east with the speed (${v_w}$) of $25m/s$ . So $\overrightarrow {{v_w}} = 25i$ $m/s$ .
If the velocity of the rain as experienced by a person standing on ground is ${v_{rw}}$ then we can represent it by the following vector diagram.

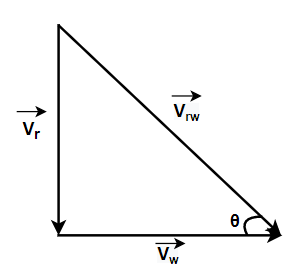
Here $\theta$ is the angle between the resultant vector and the ground.
So,
$\tan \theta = \dfrac{{\overrightarrow {{v_r}} }}{{\overrightarrow {{v_w}} }} \\\ \Rightarrow \tan \theta = \dfrac{{25\sqrt 3 }}{{25}} = \sqrt 3 \\\$
Now $\theta = \dfrac{\pi }{3}$
According to the Triangle law of vector addition states that when two vectors are represented as two sides of the triangle with the order of the magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector.
Applying Triangle law, we can say $\overrightarrow {{v_{rw}}} = \overrightarrow {{v_r}} + \overrightarrow {{v_w}}$
So, $\overrightarrow {{v_{rw}}} = 25i + 25\sqrt 3 j$ $m/s$
Now $\left| {\overrightarrow {{v_{rw}}} } \right| = \sqrt {{{(25)}^2} + {{(25\sqrt 3 )}^2}}$ $m/s$
$= \sqrt {4 \times {{25}^2}}$ $m/s$
$= 50$ $m/s$
Therefore, the velocity of the rain as experienced by a person standing on ground is $50m/s$ and it makes angle $\dfrac{\pi }{3}$ with the ground.

So, the correct answer is option A.

Note:
Relative velocity is the velocity of an object that is observed from a particular reference frame. It varies with the choice of the reference frame. Drawing a vector diagram, showing the velocity vectors can help in understanding the relative velocity.