Question

Rain is falling with a speed of $12\sqrt{2}m{{s}^{-1}}$ at angle of ${{45}^{\circ }}$ with the vertical line. A man in a glider going at a speed of V at an angle of ${{37}^{\circ }}$ with respect to the ground. Find the speed of the glider so that rain appears to him falling vertically. Consider the motion of the glider and rain drops in the same vertical plane.

a.) $15m{{s}^{-1}}$
b.) $30m{{s}^{-1}}$
c.) $10m{{s}^{-1}}$
d.) $25m{{s}^{-1}}$

Answer 1

In this question rain is falling due to gravity but we are not going to take any factor of acceleration due to gravity as we have been given a constant speed of rain and this is also known as terminal velocity. When raindrops fall, they attain a certain maximum frequency which is known as terminal velocity and this remains constant

Complete answer:
We have been given that velocity or rain (${{V}_{r}}$) is equal to $12\sqrt{2}m{{s}^{-1}}$ and Rain is making an angle of ${{45}^{\circ }}$
We have also been given that a man with velocity V is gliding by making an angle of ${{37}^{\circ }}$
Since in the question we are given with two different figures and hence to solve this question we need to make a separate figure which will be the combination of both the figure and will help us in solving the question
Now, the above figure can be simplified as

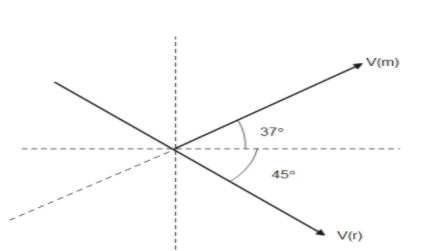
Here ${{V}_{r}}$ denotes the velocity of Rain and ${{V}_{m}}$ denotes the velocity of man
Now for the raindrops to appear like falling vertically, ${{V}_{rm}}$ should be in vertical direction
Now the figure becomes

${{V}_{rm}}={{V}_{r}}-{{V}_{m}}$
${{V}_{rm}}={{V}_{r}}+(-{{V}_{m}})$
To satisfy the condition in above equation, the components of both the velocities should cancel each other
So, we can write
${{V}_{m}}\cos {{37}^{\circ }}={{V}_{r}}\cos {{45}^{\circ }}$
Putting the values in this equation we get,
${{V}_{m}}=15m{{s}^{-1}}$

Hence, Option (a) is the correct answer

Note:
All the Velocities are measured with respect to the ground and hence we can assume that our ground is at rest. So, we took the ground as the observing frame of reference because the observation will be different in different frame of reference and hence it is necessary to take a stable frame of reference to solve the question