Solveeit Logo
Login

Question

Question: Rain is falling vertically with a speed of \(35m{s^{ - 1}}\). Winds start blowing after some time wi...

Rain is falling vertically with a speed of 35ms−135m{s^{ - 1}}. Winds start blowing after some time with a speed of 12ms−112m{s^{ - 1}}in east to west direction. At what angle with the vertical should a boy waiting at a bus stop should hold his umbrella to protect himself from rain?
A. sin⁡−1(1235){\sin ^{ - 1}}\left( {\dfrac{{12}}{{35}}} \right)
B. cos⁡−1(1235){\cos ^{ - 1}}\left( {\dfrac{{12}}{{35}}} \right)
C. tan⁡−1(1235){\tan ^{ - 1}}\left( {\dfrac{{12}}{{35}}} \right)
D. cot⁡−1(1235){\cot ^{ - 1}}\left( {\dfrac{{12}}{{35}}} \right)

Explanation

Solution

Here, speed of rain and speed of wind is given. We know that rain falls vertically downwards and it is given that wind blows in east to west direction. We need to find the resultant velocity of rain and wind to determine the angle with the vertical at which a boy should hold his umbrella to protect himself from rain.

Formula used:
vAB→=vA→+vB→\overrightarrow {{v_{AB}}} = \overrightarrow {{v_A}} + \overrightarrow {{v_B}} , where, vAB→\overrightarrow {{v_{AB}}} is the resultant velocity of A and B, vA→\overrightarrow {{v_A}} is the velocity of A and vB→\overrightarrow {{v_B}} is the velocity of B

Complete step by step answer:
It is given that Rain is falling vertically at speed of 35ms−135m{s^{ - 1}} and wind is blowing with velocity 12ms−112m{s^{ - 1}}in the direction of east to west.

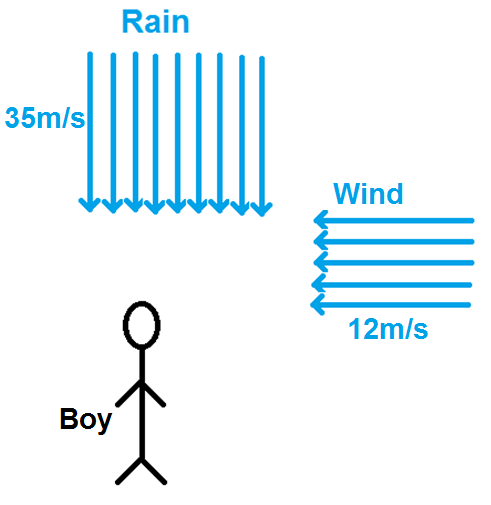
From the figure, we can say that,
Velocity of rain vr→=−35j^m/s\overrightarrow {{v_r}} = - 35\widehat jm/sand velocity of wind vw→=−12i^m/s\overrightarrow {{v_w}} = - 12\widehat im/s
Now, we will find the resultant velocity of rain and wind.
By using the formula vAB→=vA→+vB→\overrightarrow {{v_{AB}}} = \overrightarrow {{v_A}} + \overrightarrow {{v_B}} ,
vrw→=vr→+vw→\overrightarrow {{v_{rw}}} = \overrightarrow {{v_r}} + \overrightarrow {{v_w}} , where, vrw→\overrightarrow {{v_{rw}}} is the resultant velocity of rain and wind
vrw→=vr→+vw→=−35j^−12i^\overrightarrow {{v_{rw}}} = \overrightarrow {{v_r}} + \overrightarrow {{v_w}} = - 35\widehat j - 12\widehat i
If we draw a vector diagram for this resultant velocity of rain and wind, we get

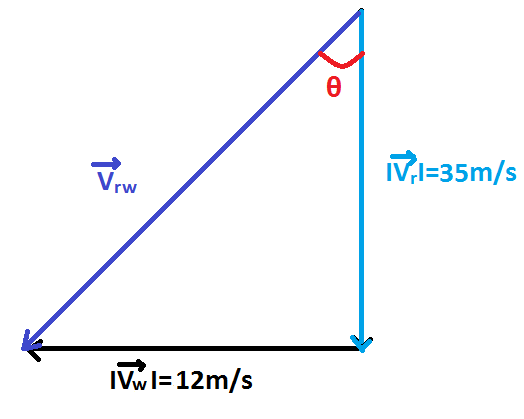
The direction of the resultant velocity of rain and wind should be the opposite direction of holding an umbrella.
From the figure,
tan⁡θ=1235 ⇒θ=tan⁡−1(1235)  \tan \theta = \dfrac{{12}}{{35}} \\\ \Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{{12}}{{35}}} \right) \\\
This angle is vertical.

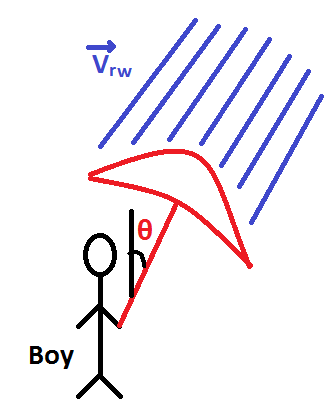
Thus, as shown in figure, a boy should hold the umbrella with the angle θ=tan⁡−1(1235)\theta = {\tan ^{ - 1}}\left( {\dfrac{{12}}{{35}}} \right) protect himself from rain.

So, the correct answer is “Option C”.

Note:
Here we have used the concept of resultant velocity to determine the angle at which the boy should hold his umbrella to protect himself from getting wet. This is because the velocity of wind in east to west direction affects the raindrops. Thus, by adding the velocity of wind to that of the rain, we determined the resultant velocity by the help of which we have determined the required angle.