Question

Rain is falling vertically with a speed of $20m/s$ relative to air. A person is running in the rain with a velocity of $5m/s$ and a wind is also blowing with a speed of $15m/s$ (both towards east). Find the tan of the angle with the vertical at which the person should hold his umbrella so that he may not get drenched.
(A) $\dfrac{1}{2}$
(B) $2$
(C) $3$
(D) $6$

Answer 1

We can make use of vectors to solve this problem. The rain is falling vertically downwards and both the man and the wind are moving in the same direction towards east. We know if two vectors are in the same direction they get added up. So, we now have two vectors one downwards and one towards east. But we will have to look at the relative velocities too. They are perpendicular to each other and so we can find the resultant vector easily using the law of vector addition.

Complete Step By Step Solution:

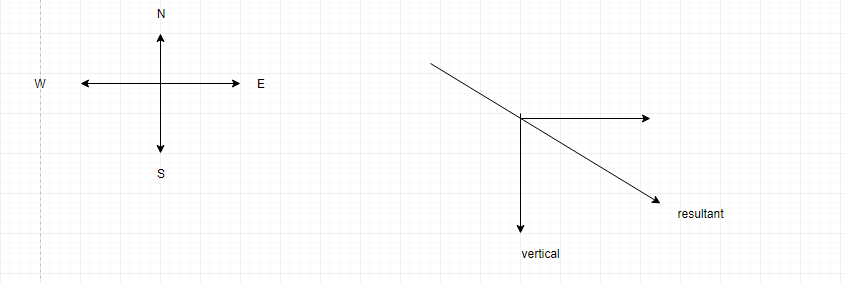
Let E be along positive x-axis and vertically up be along positive y-axis
Velocity of rain, ${{\overrightarrow{v}}_{r}}=-20\widehat{j}m/s$
Velocity of wind is ${{\overrightarrow{v}}_{W}}=15\widehat{i}m/s$ and velocity of man is ${{\overrightarrow{v}}_{m}}=15\widehat{i}m/s$
Let us find the resultant wind and the rain. Now the angle between the two vectors is ${{90}^{0}}$
\Rightarrow \overrightarrow{{{v}_{0}}}=\overrightarrow{{{v}_{r}}}-\overrightarrow{{{v}_{w}}} \\\ \Rightarrow \overrightarrow{{{v}_{0}}}=-20\widehat{j}+15\widehat{i} \\\
Now we find the resultant of this vector and the man:
\Rightarrow \overrightarrow{{{v}_{0}}'}=5\widehat{i}-(-20\widehat{k}+15\widehat{i}) \\\ \therefore \overrightarrow{{{v}_{0}}'}=-10\widehat{i}+20\widehat{j} \\\
Now, we see Tan of angle from vertical at which the person should hold his umbrella: $\tan \theta =\dfrac{10}{20}=\dfrac{1}{2}$

So, the correct option is (a)

Note: Special care should be taken while resolving the vectors and the sign of directions are to be included respectively as positive or negative. While taking trigonometric ratios see for angle and how it is made whether with horizontal or vertical
Also, the angle could be made with the horizontal or with the vertical as per the convenience of the demand of the question.