Question

Railway tracks are banked on curves
A. necessary centrifugal force may be obtained from the horizontal component weight of the train
B. to avoid frictional force between the tracks and wheels
C. necessary centripetal force may be obtained from the horizontal component of the weight of the train
D. the train may not fly off in the opposite direction

Answer 1

Hint :
Making a free body diagram will help in understanding how the banking of roads at curves helps. The reason behind banking in railway track curves is exactly the same behind banking in roads. We will equate the forces acting on the train to get the solution. The centripetal force acts towards the center of the circle and the centrifugal force away from the center.

Step by step solution:
Let’s start by making a free body diagram of a train being banked upon passing through a curve of radius (r). Let the train be travelling with velocity (v) and the acceleration acting downwards is (g). Further, let the mass of the train be (m) and the angle of inclination, that is banking angle be $'\theta '.$

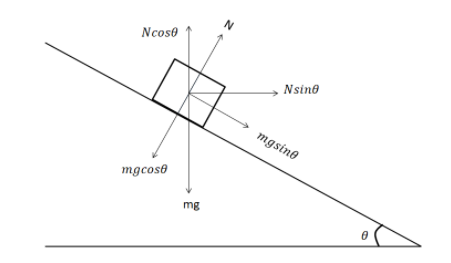
Due to the circular motion of the train travelling through a curve, a centrifugal force would act on the train away from the center of the curve of the railway track. Similarly, the frictional force $({{F}_{\mu }})$ between the tracks and the wheels of the train along with the centripetal force counteracts this centrifugal force.
From the free body diagram, we find that the horizontal component of the mass of the train acting on the train, adds to the force acting towards the center of the curve, known as the centripetal force.
Hence, the net amount of force acting towards the center, that is the centripetal force becomes: ${{F}_{C}}={{F}_{\mu }}+mg\sin \theta$. Hence, an additional component ($mg\sin \theta$), provides additional centripetal force, so that the train doesn’t derail upon travelling upon the curves.
Therefore Option C is the solution.

Note :
To find out the banking angle, we’ve already considered the mass of the train travelling along the railway curve is ‘m’. Using the same radius of curvature ‘r’, velocity of the train ‘v’, acceleration due to gravity ‘g’ and the angle on inclination is$'\theta '.$
The centripetal force acting on the train will be equated against the horizontal component of Normal.
$N\sin \theta =ma\Rightarrow N\sin \theta =\dfrac{m{{v}^{2}}}{r}$and$N\cos \theta =mg$
Dividing the above 2 equations, we get,$\tan \theta =\dfrac{{{v}^{2}}}{rg}$. Hence, the optimum or the minimum banking angle is $\theta ={{\tan }^{-1}}(\dfrac{{{v}^{2}}}{rg})$.