Question

Radius of the largest circle which passes through the focus of the parabola ${{y}^{2}}=4x$ and contained in it, is
(a). 8
(b). 4
(c). 2
(d). 5

Answer 1

Hint: To find the radius of the largest circle which passes through the focus of the parabola and is contained in the parabola, we will find the centre of the parabola by making the general equation of circle pass through the focus of the parabola and solve it in terms of radius of the circle.

Complete step by step answer:
We have the equation of parabola as ${{y}^{2}}=4x$.
We want to find the radius of the largest circle which passes through the focus of the parabola.
We know the focus of the parabola of the form ${{y}^{2}}=4ax$ is $(a,0)$ .
Thus, the focus of the parabola ${{y}^{2}}=4x$ is $(1,0)$ .

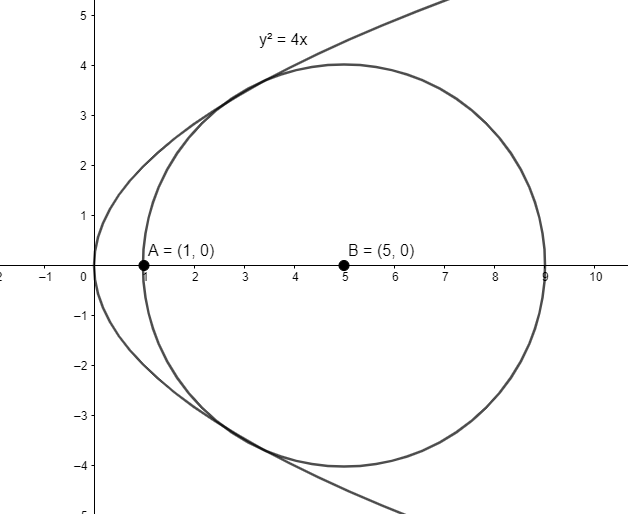
As we want the largest circle contained in parabola ${{y}^{2}}=4x$ and the circle passes through focus of parabola, the centre of the circle lies on $x$ -axis.
Let’s assume that the centre of the circle is $(h,0)$ .
Let the radius of the circle be $r$ .
As the circle passes through $(1,0)$ , we have $h=1+r$ . $(1)$
We know the equation of circle passing through the point $(h,k)$ is of the form ${{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}$ .
So, the equation of our circle is ${{(x-h)}^{2}}+{{y}^{2}}={{r}^{2}}$
Substituting the value of $h$ from equation $(1)$ , we get ${{(x-1-r)}^{2}}+{{y}^{2}}={{r}^{2}}$ .
$\Rightarrow {{x}^{2}}+{{r}^{2}}+1-2x-2xr+2r+{{y}^{2}}={{r}^{2}}$
$\Rightarrow {{x}^{2}}+{{y}^{2}}-2x-2xr+1+2r=0$
But, we know ${{y}^{2}}=4x$ . Substituting this in the above equation, we get ${{x}^{2}}+4x-2x-2xr+1+2r=0$ .
$\Rightarrow {{x}^{2}}+2x-2xr+1+2r=0$ $(2)$
The above quadratic equation will have equal roots because the circle intersects the parabola.
We know that when the quadratic equation of the form $a{{x}^{2}}+bx+c=0$ has equal roots, we have ${{b}^{2}}-4ac=0$ .
Substituting $b=2-2r,c=1+2r$ from equation $(2)$ to the above formula, we get ${{(2-2r)}^{2}}=4(1+2r)$ .
On further solving this equation, we get

& \Rightarrow 4+4{{r}^{2}}-8r=4+8r \\\ & \Rightarrow 4{{r}^{2}}-16r=0 \\\ & \Rightarrow 4r(r-4)=0 \\\ & \Rightarrow r=0,r=4 \\\ \end{aligned}$$ But the radius of the circle can’t be 0, so, the required answer is $$r=4$$ . Hence, the correct answer is 4. Note: We can’t solve the question without the fact that the circle passes through the focus of the parabola and touches the parabola at some point. Also, one must know that a circle with 0 radius is just a point.