Question

Radius of the largest circle which passes through the focus of the parabola ${{y}^{2}}=4x$ and contained in it is:
(a) $16$
(b) $5$
(c) $8$
(d) $4$

Answer 1

Hint: The equation of circle to be considered is ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. Since the given parabola lies along the y-axis, the largest possible circle passing through the focus of the parabola would have its centre on the x-axis. So, we can take the centre as $\left( b,0 \right)$.

Complete step-by-step solution -
The equation of the parabola given in the question is ${{y}^{2}}=4x$.
We know that the general equation of the parabola is given by ${{y}^{2}}=4ax$. On comparing the parabola in the question with the general form, we get $a=1$.
We also know that the focus of the parabola ${{y}^{2}}=4ax$ is $\left( a,0 \right)$. Therefore, the focus for the parabola ${{y}^{2}}=4x$ can be obtained as $\left( 1,0 \right)$. Let us denote the focus by point $B$ such that we get $AB=1$, as in the figure below.

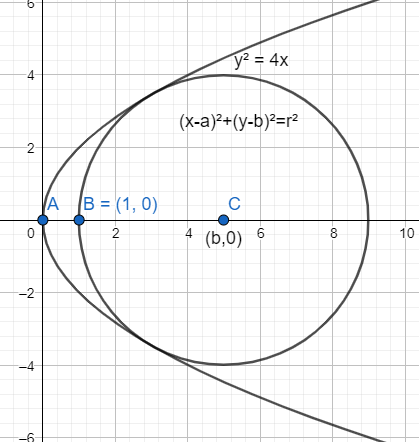
We know that the general equation of a circle is given by ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. Let us consider a circle with center $\left( b,0 \right)$. As it is contained in the parabola, by referring to the figure, we can write the radius as $BC=AC-AB$. Therefore, we get the radius as $r=b-1$.
Now, we can write the equation of the required circle as

& {{\left( x-b \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( b-1 \right)}^{2}} \\\ & {{\left( x-b \right)}^{2}}+{{y}^{2}}={{\left( b-1 \right)}^{2}} \\\ \end{aligned}$$ We also know that the circle touches the parabola ${{y}^{2}}=4x$. So, we can substitute ${{y}^{2}}=4x$ in the equation above. So, we get $${{\left( x-b \right)}^{2}}+4x={{\left( b-1 \right)}^{2}}$$ We know that $r=b-1$, so we get $b=r+1$. Now substituting this in the equation above, we get $$\begin{aligned} & {{\left( x-\left( r+1 \right) \right)}^{2}}+4x={{\left( \left( r+1 \right)-1 \right)}^{2}} \\\ & {{\left( x-\left( r+1 \right) \right)}^{2}}+4x={{\left( r \right)}^{2}} \\\ \end{aligned}$$ Since we know that $${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$$, we get $${{x}^{2}}-2x\left( r+1 \right)+{{\left( r+1 \right)}^{2}}+4x={{r}^{2}}$$ Since we know that $${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$$, we get $$\begin{aligned} & {{x}^{2}}-2xr-2x+{{r}^{2}}+2r+1+4x={{r}^{2}} \\\ & {{x}^{2}}-2xr+2x+2r+1=0 \\\ & {{x}^{2}}+x\left( 2-2r \right)+2r+1=0 \\\ \end{aligned}$$ In the obtained quadratic equation, we have to put discriminant $=0$ as it will have equal roots because the circle is contained in the parabola. $$\begin{aligned} & {{b}^{2}}-4ac=0 \\\ & {{\left( 2-2r \right)}^{2}}-4\times 1\times \left( 2r+1 \right)=0 \\\ \end{aligned}$$ Since we know that $${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$$, we get $$\begin{aligned} & 4-8r+4{{r}^{2}}-8r-4=0 \\\ & 4{{r}^{2}}-16r=0 \\\ & 4r\left( r-4 \right)=0 \\\ \end{aligned}$$ Therefore, we can get two values as $$r=0,r=4$$. Since the radius can’t be zero, we get the radius of the circle as $$4$$. _Therefore, we get option (d) as the correct answer._ Note: In this question, we have to find the radius of the largest circle contained in the parabola. For that, we have to equate the discriminant = 0 as it is the condition for equal roots. If we consider the value of the radius as zero, it becomes a point circle.