Question

$r_1$ = _____$\Omega$

15. The figure shows a circuit having eight resistances of 1$\Omega$ each, labelled $R_1$ to $R_8$, and two ideal batteries with voltages $\varepsilon_1$ = 12V and $\varepsilon_2$ = 6V. [2022]

Which of the following statement(s) is(are) correct?

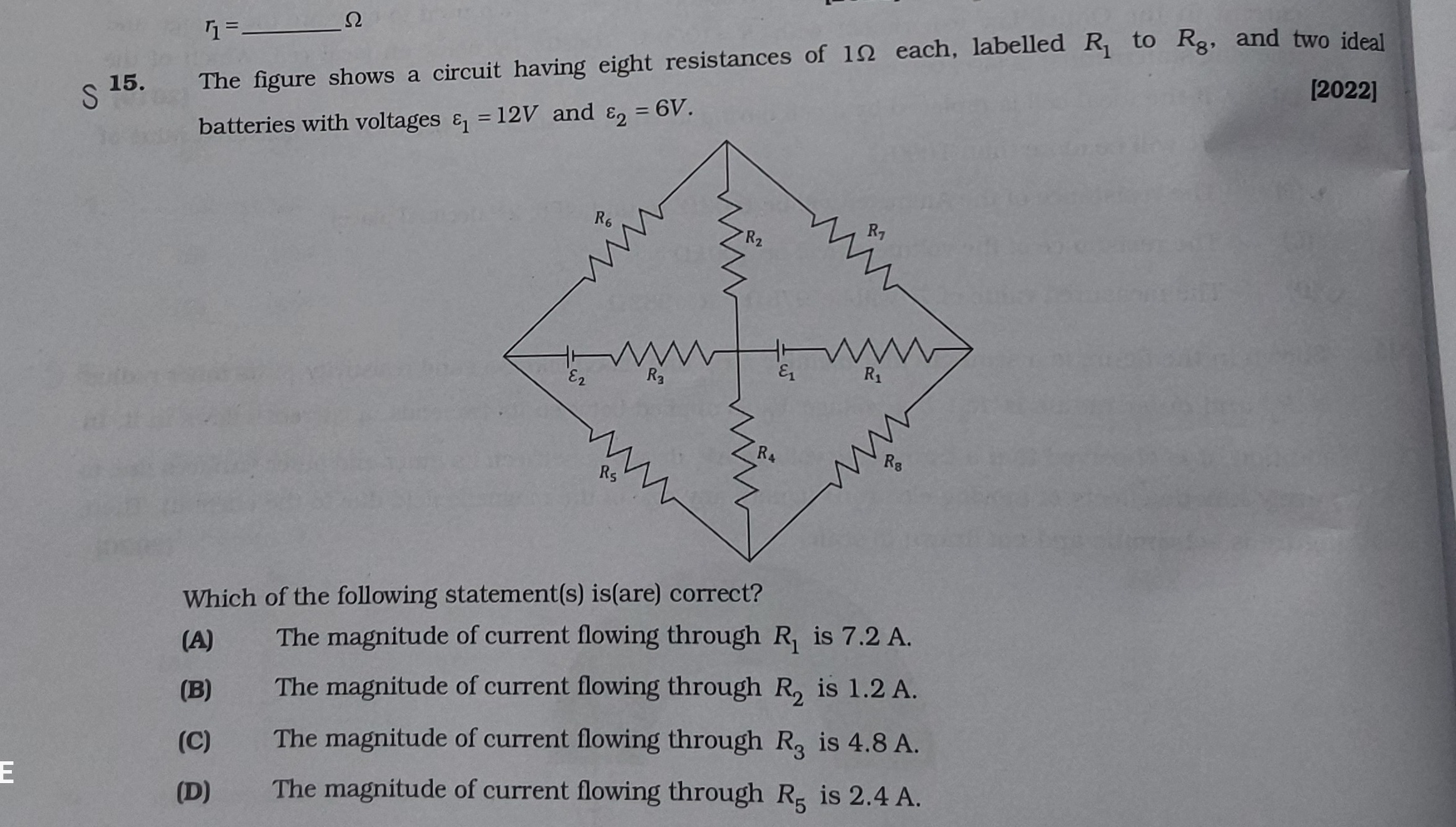
• A. The magnitude of current flowing through $R_1$ is 7.2 A.
• B. The magnitude of current flowing through $R_2$ is 1.2 A.
• C. The magnitude of current flowing through $R_3$ is 4.8 A.
• D. The magnitude of current flowing through $R_5$ is 2.4 A.

Answer 1

No correct option

Answer 2

1. Node Definition: Assign potentials to the key nodes: $V_T$ (top), $V_L$ (left-center), $V_R$ (right-center), $V_C$ (central), and $V_0 = 0V$ (bottom reference).

2. Battery Relations: From the ideal batteries, establish potential differences: $V_R - V_C = 12V \implies V_R = V_C + 12$ $V_L - V_C = 6V \implies V_L = V_C + 6$

3. KCL at $V_T$: Sum of currents leaving $V_T$ is zero. All resistances are $1\Omega$. $(V_T - V_C) + (V_T - V_L) + (V_T - V_R) = 0$ $3V_T - V_C - (V_C + 6) - (V_C + 12) = 0 \implies 3V_T - 3V_C - 18 = 0 \implies V_T = V_C + 6$.

4. KCL for Supernode ($V_L, V_R, V_C$): Sum of currents leaving the supernode through external resistors is zero. $(V_L - V_T) + (V_L - V_0) + (V_R - V_T) + (V_R - V_0) + (V_R - V_0) + (V_C - V_T) + (V_C - V_0) = 0$ $2V_L + 3V_R + 2V_C - 3V_T - 3V_0 = 0$ Substitute $V_0=0$, $V_L = V_C + 6$, $V_R = V_C + 12$, $V_T = V_C + 6$: $2(V_C + 6) + 3(V_C + 12) + 2V_C - 3(V_C + 6) = 0$ $2V_C + 12 + 3V_C + 36 + 2V_C - 3V_C - 18 = 0$ $4V_C + 30 = 0 \implies V_C = -7.5V$.

5. Calculate Node Potentials: $V_C = -7.5V$ $V_R = -7.5 + 12 = 4.5V$ $V_L = -7.5 + 6 = -1.5V$ $V_T = -7.5 + 6 = -1.5V$ $V_0 = 0V$

6. Calculate Currents: (Magnitude is $|\Delta V|/R$) (A) Current through $R_1$: $|V_R - V_0| / R_1 = |4.5 - 0| / 1 = 4.5A$. (Option A is 7.2A) (B) Current through $R_2$: $|V_T - V_C| / R_2 = |-1.5 - (-7.5)| / 1 = |6.0| / 1 = 6.0A$. (Option B is 1.2A) (C) Current through $R_3$: $|V_R - V_L| / R_3 = |4.5 - (-1.5)| / 1 = |6.0| / 1 = 6.0A$. (Option C is 4.8A) (D) Current through $R_5$: $|V_L - V_0| / R_5 = |-1.5 - 0| / 1 = 1.5A$. (Option D is 2.4A)

Based on the calculations, none of the given options are correct.