Question
Question: The alternative that gives the conservative force of the following is:...
The alternative that gives the conservative force of the following is:
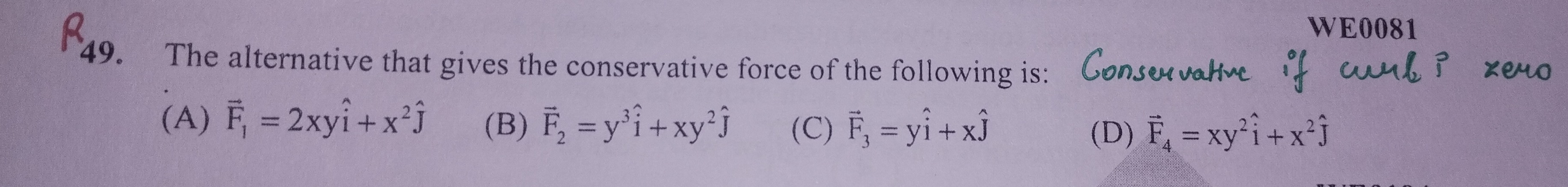
F1=2xyi^+x2j^
F2=y3i^+xy2j^
F3=yi^+xj^
F4=xy2i^+x2j^
A and C
Solution
A force F=Fxi^+Fyj^ is conservative if its curl is zero. For a two-dimensional force, this condition simplifies to ∂x∂Fy=∂y∂Fx.
We check this condition for each option: (A) F1=2xyi^+x2j^: Fx=2xy, Fy=x2. ∂y∂Fx=∂y∂(2xy)=2x. ∂x∂Fy=∂x∂(x2)=2x. Since ∂x∂Fy=∂y∂Fx (both are 2x), F1 is a conservative force.
(B) F2=y3i^+xy2j^: Fx=y3, Fy=xy2. ∂y∂Fx=∂y∂(y3)=3y2. ∂x∂Fy=∂x∂(xy2)=y2. Since ∂x∂Fy=∂y∂Fx (y2=3y2), F2 is not a conservative force.
(C) F3=yi^+xj^: Fx=y, Fy=x. ∂y∂Fx=∂y∂(y)=1. ∂x∂Fy=∂x∂(x)=1. Since ∂x∂Fy=∂y∂Fx (both are 1), F3 is a conservative force.
(D) F4=xy2i^+x2j^: Fx=xy2, Fy=x2. ∂y∂Fx=∂y∂(xy2)=2xy. ∂x∂Fy=∂x∂(x2)=2x. Since ∂x∂Fy=∂y∂Fx (2x=2xy), F4 is not a conservative force.
Therefore, the conservative forces are F1 and F3.
