Question

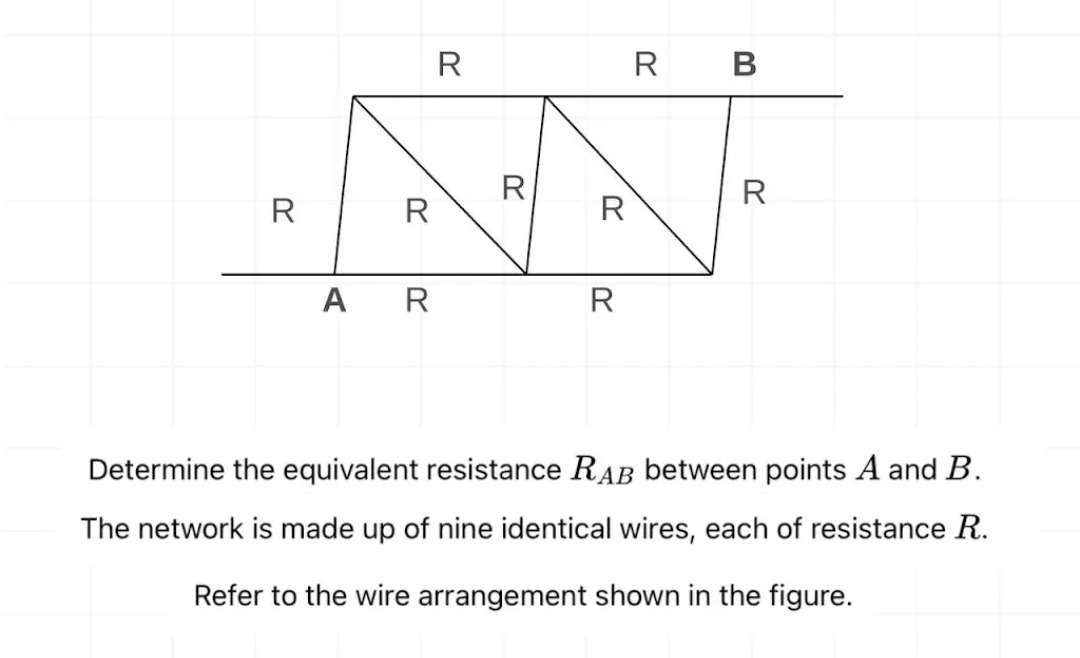
Determine the equivalent resistance $R_{AB}$ between points $A$ and $B$.

The network is made up of nine identical wires, each of resistance $R$.

Refer to the wire arrangement shown in the figure.

Answer 1

$\frac{9R}{5}$

Answer 2

The problem asks to determine the equivalent resistance $R_{AB}$ between points A and B for the given network. The network consists of wires, each of resistance $R$. The problem statement mentions "nine identical wires", but the figure clearly shows 11 wires, each labeled with resistance $R$. In such cases, the diagram is usually considered the definitive representation of the circuit. We will proceed with the assumption that there are 11 wires, each of resistance $R$, as shown in the figure.

Let's label the nodes in the circuit for clarity:

• Bottom row nodes: A, C, D, E (from left to right)
• Top row nodes: F, G, H, B (from left to right)

The resistances are connected as follows:

1. $R_{AC} = R$
2. $R_{CD} = R$
3. $R_{DE} = R$
4. $R_{AF} = R$
5. $R_{EB} = R$
6. $R_{FG} = R$
7. $R_{GH} = R$
8. $R_{HB} = R$
9. $R_{CG} = R$ (diagonal)
10. $R_{DG} = R$ (diagonal)
11. $R_{DH} = R$ (diagonal)

To find the equivalent resistance $R_{AB}$, we can use the node voltage method. Let's assume a potential $V_A = 0$ at node A and $V_B = V$ at node B. We need to find the total current $I$ flowing from A to B, then $R_{AB} = V/I$.

Let $V_C, V_D, V_E, V_F, V_G, V_H$ be the potentials at nodes C, D, E, F, G, H respectively. Applying Kirchhoff's Current Law (KCL) at each node (sum of currents leaving the node is zero):

1. Node C: $\frac{V_C - V_A}{R} + \frac{V_C - V_D}{R} + \frac{V_C - V_G}{R} = 0$ Since $V_A = 0$: $V_C + (V_C - V_D) + (V_C - V_G) = 0 \implies 3V_C - V_D - V_G = 0$ (Eq. 1)

2. Node D: $\frac{V_D - V_C}{R} + \frac{V_D - V_E}{R} + \frac{V_D - V_G}{R} + \frac{V_D - V_H}{R} = 0$ $4V_D - V_C - V_E - V_G - V_H = 0$ (Eq. 2)

3. Node E: $\frac{V_E - V_D}{R} + \frac{V_E - V_B}{R} = 0$ Since $V_B = V$: $(V_E - V_D) + (V_E - V) = 0 \implies 2V_E - V_D - V = 0$ (Eq. 3) From Eq. 3, $V_E = \frac{V_D + V}{2}$

4. Node F: $\frac{V_F - V_A}{R} + \frac{V_F - V_G}{R} = 0$ Since $V_A = 0$: $V_F + (V_F - V_G) = 0 \implies 2V_F - V_G = 0$ (Eq. 4) From Eq. 4, $V_F = \frac{V_G}{2}$

5. Node G: $\frac{V_G - V_F}{R} + \frac{V_G - V_C}{R} + \frac{V_G - V_D}{R} + \frac{V_G - V_H}{R} = 0$ $4V_G - V_F - V_C - V_D - V_H = 0$ (Eq. 5)

6. Node H: $\frac{V_H - V_G}{R} + \frac{V_H - V_D}{R} + \frac{V_H - V_B}{R} = 0$ Since $V_B = V$: $(V_H - V_G) + (V_H - V_D) + (V_H - V) = 0 \implies 3V_H - V_G - V_D - V = 0$ (Eq. 6)

Now, substitute $V_E$ from Eq. 3 and $V_F$ from Eq. 4 into Eq. 2 and Eq. 5:

Substitute $V_E$ into Eq. 2: $4V_D - V_C - \left(\frac{V_D + V}{2}\right) - V_G - V_H = 0$ Multiply by 2: $8V_D - 2V_C - (V_D + V) - 2V_G - 2V_H = 0$ $7V_D - 2V_C - 2V_G - 2V_H = V$ (Eq. 2')

Substitute $V_F$ into Eq. 5: $4V_G - \left(\frac{V_G}{2}\right) - V_C - V_D - V_H = 0$ Multiply by 2: $8V_G - V_G - 2V_C - 2V_D - 2V_H = 0$ $7V_G - 2V_C - 2V_D - 2V_H = 0$ (Eq. 5')

Now we have a system of four linear equations (Eq. 1, Eq. 2', Eq. 5', Eq. 6) with four unknowns ($V_C, V_D, V_G, V_H$). Let's divide all equations by $V$ and let $v_x = V_x/V$ for simplicity. So $v_A=0$ and $v_B=1$.

1. $3v_C - v_D - v_G = 0$
2. $-2v_C + 7v_D - 2v_G - 2v_H = 1$
3. $-2v_C - 2v_D + 7v_G - 2v_H = 0$
4. $-v_D - v_G + 3v_H = 1$

From (1), $v_G = 3v_C - v_D$. Substitute this into (2), (3), (4):

Substitute into (2): $-2v_C + 7v_D - 2(3v_C - v_D) - 2v_H = 1$ $-2v_C + 7v_D - 6v_C + 2v_D - 2v_H = 1$ $-8v_C + 9v_D - 2v_H = 1$ (Eq. A)

Substitute into (3): $-2v_C - 2v_D + 7(3v_C - v_D) - 2v_H = 0$ $-2v_C - 2v_D + 21v_C - 7v_D - 2v_H = 0$ $19v_C - 9v_D - 2v_H = 0$ (Eq. B)

Substitute into (4): $-v_D - (3v_C - v_D) + 3v_H = 1$ $-v_D - 3v_C + v_D + 3v_H = 1$ $-3v_C + 3v_H = 1$ (Eq. C)

Now we have a system of three equations (A, B, C) with three unknowns ($v_C, v_D, v_H$). From (C), $3v_H = 1 + 3v_C \implies v_H = \frac{1}{3} + v_C$. Substitute $v_H$ into (A) and (B):

Substitute into (A): $-8v_C + 9v_D - 2\left(\frac{1}{3} + v_C\right) = 1$ $-8v_C + 9v_D - \frac{2}{3} - 2v_C = 1$ $-10v_C + 9v_D = 1 + \frac{2}{3} = \frac{5}{3}$ (Eq. A')

Substitute into (B): $19v_C - 9v_D - 2\left(\frac{1}{3} + v_C\right) = 0$ $19v_C - 9v_D - \frac{2}{3} - 2v_C = 0$ $17v_C - 9v_D = \frac{2}{3}$ (Eq. B')

Now we have a system of two equations (A', B') with two unknowns ($v_C, v_D$). Add (A') and (B'): $(-10v_C + 9v_D) + (17v_C - 9v_D) = \frac{5}{3} + \frac{2}{3}$ $7v_C = \frac{7}{3}$ $v_C = \frac{1}{3}$

Substitute $v_C = \frac{1}{3}$ into (A'): $-10\left(\frac{1}{3}\right) + 9v_D = \frac{5}{3}$ $-\frac{10}{3} + 9v_D = \frac{5}{3}$ $9v_D = \frac{15}{3} = 5$ $v_D = \frac{5}{9}$

Now find $v_H$ using $v_H = \frac{1}{3} + v_C$: $v_H = \frac{1}{3} + \frac{1}{3} = \frac{2}{3}$

Now find $v_G$ using $v_G = 3v_C - v_D$: $v_G = 3\left(\frac{1}{3}\right) - \frac{5}{9} = 1 - \frac{5}{9} = \frac{4}{9}$

Now find $v_F$ using $v_F = \frac{v_G}{2}$: $v_F = \frac{4/9}{2} = \frac{2}{9}$

Now find $v_E$ using $v_E = \frac{v_D + 1}{2}$: $v_E = \frac{5/9 + 1}{2} = \frac{14/9}{2} = \frac{7}{9}$

So, the potentials relative to $V$ (where $V_A=0, V_B=V$) are: $V_C = V/3$ $V_D = 5V/9$ $V_E = 7V/9$ $V_F = 2V/9$ $V_G = 4V/9$ $V_H = 2V/3 = 6V/9$

The total current $I$ flowing from A into the network is the sum of currents through $R_{AF}$ and $R_{AC}$: $I = I_{AF} + I_{AC} = \frac{V_F - V_A}{R} + \frac{V_C - V_A}{R}$ $I = \frac{V_F}{R} + \frac{V_C}{R}$ $I = \frac{2V/9}{R} + \frac{V/3}{R} = \frac{2V}{9R} + \frac{3V}{9R} = \frac{5V}{9R}$

The equivalent resistance $R_{AB}$ is $V/I$: $R_{AB} = \frac{V}{5V/(9R)} = \frac{9R}{5}$

The final answer is $\boxed{\frac{9R}{5}}$.

Explanation of the solution:

1. Identify Nodes and Resistances: Label all junction points in the circuit. Count and confirm all resistances as shown in the diagram, ignoring the "nine identical wires" text if it contradicts the diagram.
2. Apply Node Voltage Method: Assign a reference potential (e.g., $V_A = 0$) and an unknown potential (e.g., $V_B = V$). Assign unknown potentials to all other independent nodes.
3. Formulate KCL Equations: Write Kirchhoff's Current Law equations for each unknown node, stating that the sum of currents leaving the node is zero. This will result in a system of linear equations.
4. Solve the System of Equations: Systematically solve the equations to find the potentials of all nodes in terms of $V$ and $R$.
5. Calculate Total Current: Determine the total current entering (or leaving) the network from the source node (A) or to the destination node (B). This is done by summing the currents through the resistors connected to the source/destination node.
6. Calculate Equivalent Resistance: Use Ohm's Law $R_{AB} = V/I$ to find the equivalent resistance.