Question
Question: The roots of the equation $4x^4 - 24x^3 + 57x^2 + 18x - 45 = 0$. If one of them is $3 + i\sqrt{6}$,...
The roots of the equation 4x4−24x3+57x2+18x−45=0. If one of them is 3+i6,
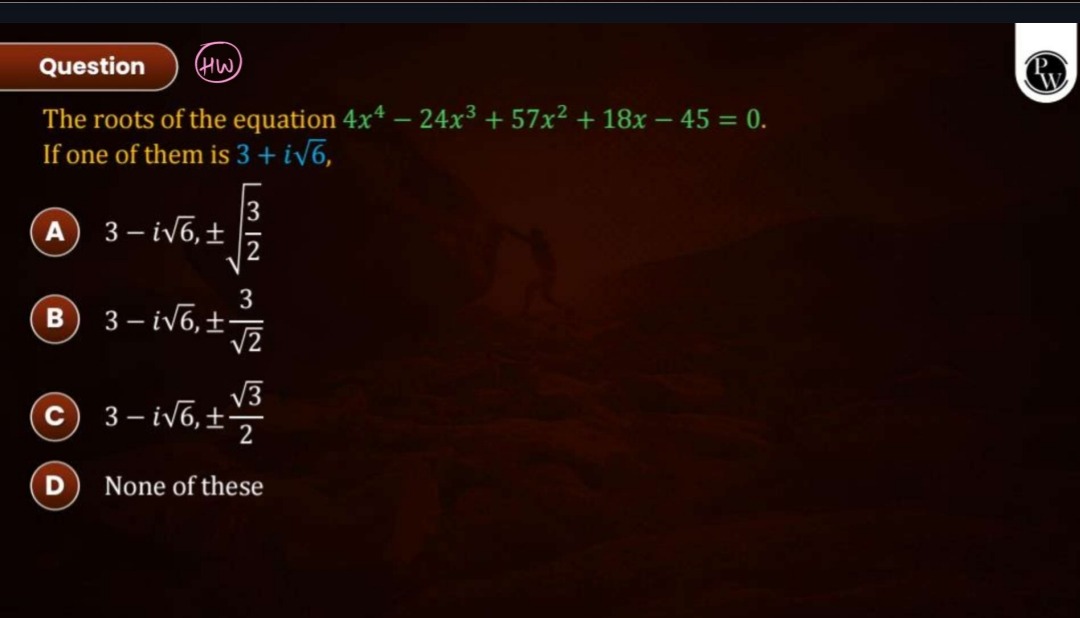
A
3−i6,±23
B
3−i6,±23
C
3−i6,±23
D
None of these
Answer
C
Explanation
Solution
Given the polynomial equation 4x4−24x3+57x2+18x−45=0.
One root is 3+i6. Since the coefficients are real, its conjugate 3−i6 must also be a root.
These two roots form a quadratic factor:
(x−(3+i6))(x−(3−i6))=(x−3)2−(i6)2=(x2−6x+9)−(−6)=x2−6x+15.
Divide the original polynomial by this factor:
(4x4−24x3+57x2+18x−45)÷(x2−6x+15)=4x2−3.
So, the equation becomes (x2−6x+15)(4x2−3)=0.
Setting the second factor to zero:
4x2−3=0⟹4x2=3⟹x2=43⟹x=±43=±23.
Thus, the roots are 3+i6, 3−i6, 23, and −23.
The roots listed in option C are 3−i6,±23, which are the remaining roots.
