Question

The value of $v_p$ is .........................

Answer 1

9.03

Answer 2

This problem involves using the Work-Energy Theorem to find the final velocity of particle P.

The Work-Energy Theorem states: $\Delta KE = W_{net}$ $\frac{1}{2}mv_f^2 - \frac{1}{2}mu_i^2 = W_{gravity} + W_{friction}$

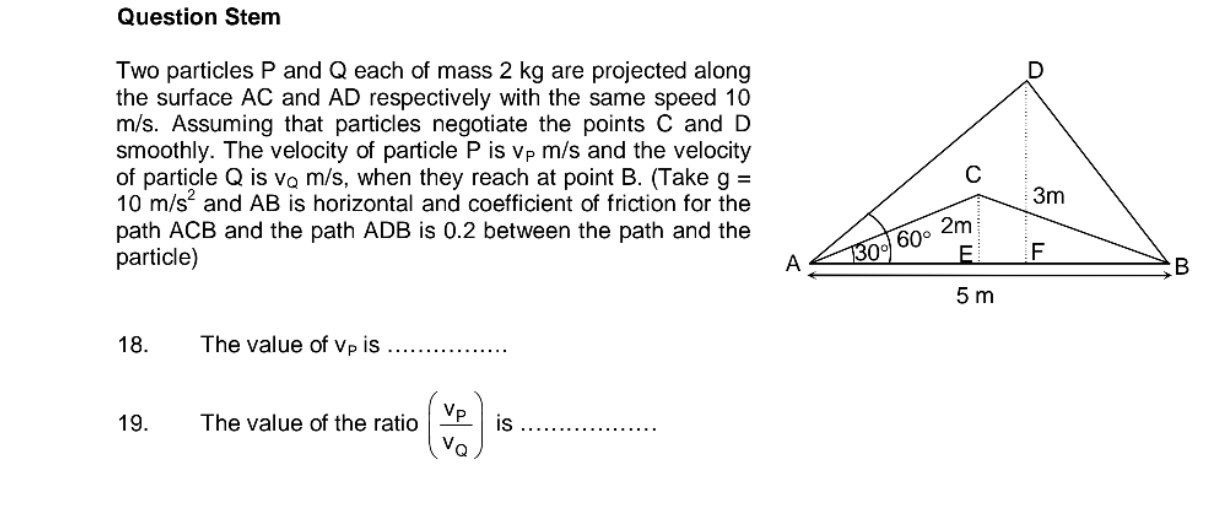
Given: Mass of particle P, $m = 2$ kg Initial speed, $u = 10$ m/s Acceleration due to gravity, $g = 10$ m/s² Coefficient of friction, $\mu = 0.2$ Initial and final points (A and B) are at the same horizontal level, so the net work done by gravity is zero ($W_{gravity} = 0$).

Therefore, the Work-Energy Theorem simplifies to: $\frac{1}{2}mv_f^2 - \frac{1}{2}mu^2 = W_{friction}$

The work done by friction on an inclined plane is given by $W_f = -f_k \times L$, where $f_k = \mu N = \mu mg \cos\theta$ and $L$ is the length of the inclined path. So, $W_f = -\mu mg \cos\theta \times L$. Since $L \cos\theta = \Delta x$ (the horizontal displacement), the work done by friction on an inclined path is $W_f = -\mu mg \Delta x$. For a path composed of multiple segments, the total work done by friction is $W_{friction} = -\mu mg \times (\text{total horizontal distance covered})$.

For Particle P (path ACB):

1. Determine path dimensions:

   • Height of C from AB, $h_C = CE = 2$ m.
   • Angle of incline for AC, $\theta_{AC} = 30^\circ$.
   • Angle of incline for CB, $\theta_{CB} = 60^\circ$.
   • Horizontal projection of AC: $AE = CE / \tan(30^\circ) = 2 / (1/\sqrt{3}) = 2\sqrt{3}$ m.
   • Horizontal projection of CB: $EB = CE / \tan(60^\circ) = 2 / \sqrt{3}$ m.
   • Total horizontal distance covered by P = $AE + EB = 2\sqrt{3} + 2/\sqrt{3} = (6+2)/\sqrt{3} = 8/\sqrt{3}$ m.

2. Calculate work done by friction: $W_{friction,P} = -\mu mg \times (\text{total horizontal distance})$ $W_{friction,P} = -0.2 \times 2 \times 10 \times (8/\sqrt{3})$ $W_{friction,P} = -4 \times (8/\sqrt{3}) = -32/\sqrt{3}$ J.

3. Apply Work-Energy Theorem: $\frac{1}{2}mv_P^2 - \frac{1}{2}mu^2 = W_{friction,P}$ $\frac{1}{2}(2)v_P^2 - \frac{1}{2}(2)(10)^2 = -32/\sqrt{3}$ $v_P^2 - 100 = -32/\sqrt{3}$ $v_P^2 = 100 - 32/\sqrt{3}$ $v_P^2 = 100 - 18.475$ $v_P^2 = 81.525$ $v_P = \sqrt{81.525} \approx 9.029$ m/s.

Therefore, the value of $v_P$ is approximately 9.03 m/s.