Question

Question: Out of two resolved components of a force, one is $10\;N$ and it makes an angle of ${60^\circ }$ with the force. The magnitude of the force is:
(A) $7.1\;N$
(B) $4.33\;N$
(C) $17.3\;N$
(D) $20\;N$

Answer 1

In physics, a vector is a physical quantity that has both magnitude and direction. It is denoted with an arrow sign on top of the quantity, for example $\vec A$. In order to signify just the magnitude of the vector, we can show this as $\left| {\left. A \right|} \right.$ or simply $A$.

Complete step by step solution:
Any vector quantity possessing a magnitude and a direction can be divided into two different components, called the rectangular components.
Similarly, the force being a vector quantity can also be divided into two different components. Here we have considered the components to be along the x-axis and the y-axis. This representation is shown in the figure below.

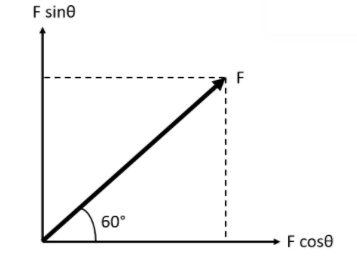
If $\theta$ be the angle made by the force vector, $\vec F$ to the x-axis, then following the figure from trigonometric properties we can see that the $x$ component of the vector is given as $F\cos \theta$, while the $y$ component is given as $F\sin \theta$.
Using these relations we are going to solve this question.
In the question, it is given that one of the components of the force if $10\;N$.
Hence we can say that any of the two rectangular components of force is $10\;N$.
Therefore let us consider the component along the x-axis to be $10\;N$.
$\therefore F\cos \theta = 10$
From the question, we know that the force vector makes an angle ${60^\circ }$ with the above vector component. Hence the above equation can be written as,
$F\cos {60^\circ } = 10$
Dividing both the sides with $\cos {60^\circ }$ we get,
$F = \dfrac{{10}}{{\cos {{60}^\circ }}}$
We know the value of $\cos {60^\circ }$ is $\dfrac{1}{2}$.
Substituting this in the above equation we get,
$F = \dfrac{{10}}{{1/2}}$
Simplifying this equation further we get,
$F = 10 \times 2$
$\therefore F = 20N$
Hence the magnitude of the given force vector is $20\;N$.

Therefore the correct answer is option (D) $20\;N$.

Note: Just like we can divide a vector into two rectangular components, we can also add two vectors with different directions into a resultant vector using the rectangle law of vector addition or subtraction. Triangle law is another method of vector addition.