Question
Question: What is the vector perpendicular to both the vectors $\vec{a} = \hat{i} - 2\hat{j} + \hat{k}$ and $\...
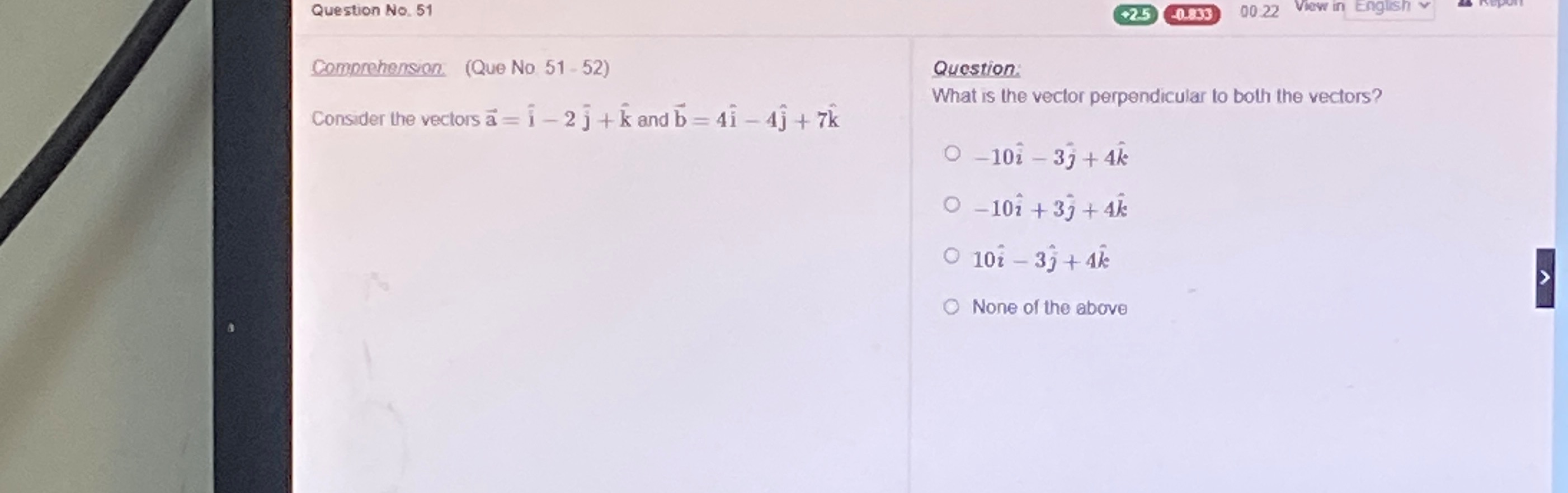
What is the vector perpendicular to both the vectors a=i^−2j^+k^ and b=4i^−4j^+7k^?
A
−10i^−3j^+4k^
B
−10i^+3j^+4k^
C
10i^−3j^+4k^
D
None of the above
Answer
−10i^−3j^+4k^
Explanation
Solution
To find a vector perpendicular to both a and b, we compute their cross product a×b.
Given vectors: a=i^−2j^+k^ b=4i^−4j^+7k^
The cross product a×b is calculated as the determinant:
a×b=i^14j^−2−4k^17Expanding the determinant:
a×b=i^((−2)(7)−(1)(−4))−j^((1)(7)−(1)(4))+k^((1)(−4)−(−2)(4)) a×b=i^(−14+4)−j^(7−4)+k^(−4+8) a×b=−10i^−3j^+4k^Thus, the vector perpendicular to both a and b is −10i^−3j^+4k^.
