Question
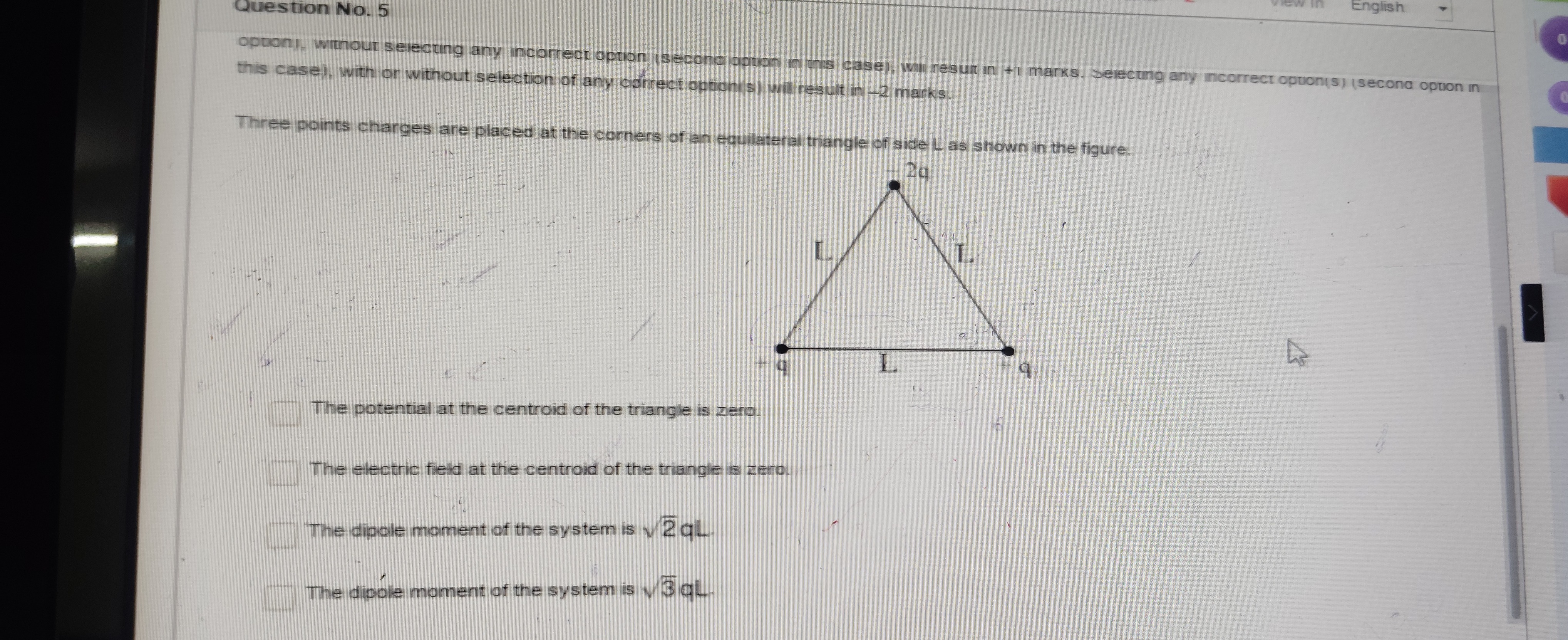
Question: Three points charges are placed at the corners of an equilateral triangle of side L as shown in the ...
Three points charges are placed at the corners of an equilateral triangle of side L as shown in the figure.
- The potential at the centroid of the triangle is zero.
- The electric field at the centroid of the triangle is zero.
- The dipole moment of the system is 2qL.
- The dipole moment of the system is 3qL.
The potential at the centroid of the triangle is zero.
The electric field at the centroid of the triangle is zero.
The dipole moment of the system is 2qL.
The dipole moment of the system is 3qL.
The potential at the centroid of the triangle is zero. The dipole moment of the system is 3qL.
Solution
Let the vertices of the equilateral triangle be A, B, and C. Assume charges +q are at A and B, and -2q is at C.
Statement 1: Potential at the centroid is zero.
The distance from each vertex to the centroid is r=3L. The potential at the centroid O is:
VO=4πϵ01(rAqA+rBqB+rCqC)
VO=4πϵ01(L/3+q+L/3+q+L/3−2q)=0
Statement 2: Electric field at the centroid is zero.
The electric field at the centroid is the vector sum of the electric fields due to each charge.
EA=4πϵ01L23q, directed away from A.
EB=4πϵ01L23q, directed away from B.
EC=4πϵ01L26q, directed towards C.
The resultant electric field is non-zero.
Statement 3 & 4: Dipole moment of the system.
The total charge of the system is 0. Place the origin at vertex C.
P=qArA+qBrB+qCrC
P=q(−L/2,L3/2)+q(L/2,L3/2)+(−2q)(0,0)
P=(0,qL3)
The magnitude of the dipole moment is ∣P∣=3qL.
Therefore, statements 1 and 4 are correct.
