Question
Question: A vector $\vec{v}$ in the plane of $\vec{a}$ and $\vec{b}$, whose projection on $\vec{c}$ is $\frac{...
A vector v in the plane of a and b, whose projection on c is 61, is given by
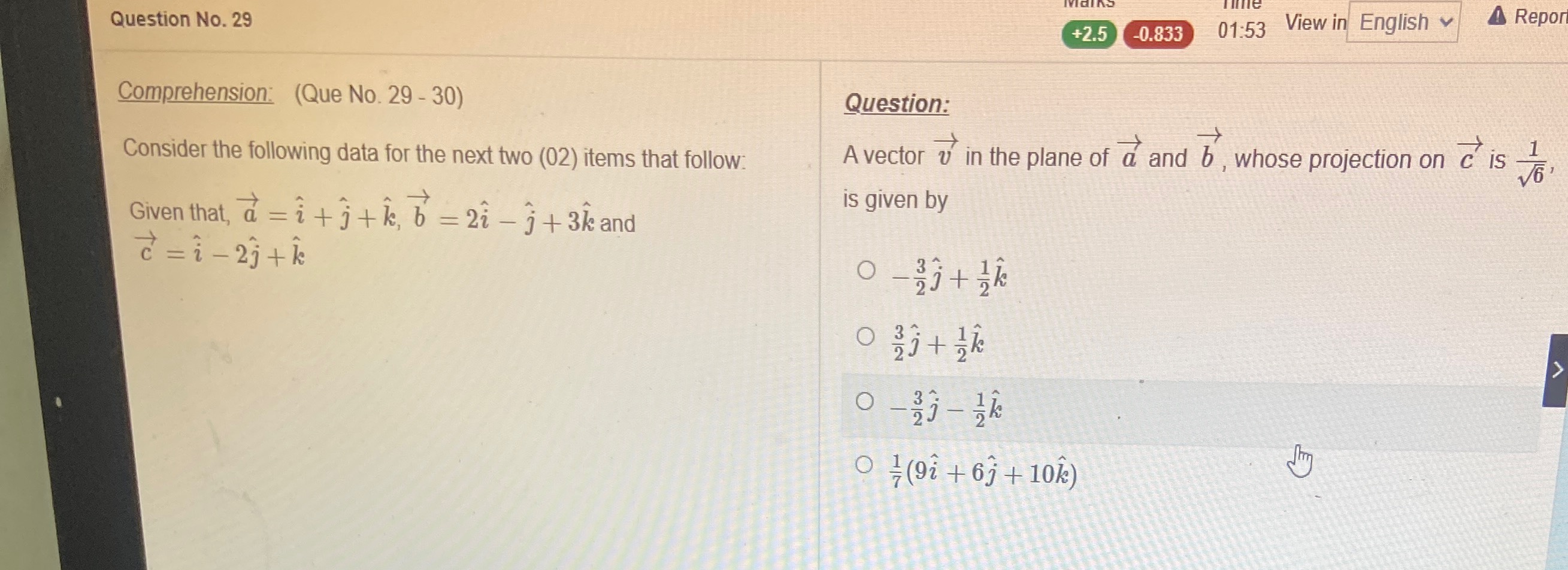
−23j^+21k^
23j^+21k^
−23j^−21k^
71(9i^+6j^+10k^)
71(9i^+6j^+10k^)
Solution
The problem asks us to find a vector v that satisfies two conditions:
- v lies in the plane of vectors a and b.
- The projection of v on vector c is 61.
Given vectors are: a=i^+j^+k^ b=2i^−j^+3k^ c=i^−2j^+k^
Step 1: Express v based on the first condition.
If v lies in the plane of a and b (assuming a and b are non-collinear, which they are, as a=kb), then v can be written as a linear combination of a and b: v=xa+yb where x and y are scalar constants.
Substitute the expressions for a and b: v=x(i^+j^+k^)+y(2i^−j^+3k^) v=(x+2y)i^+(x−y)j^+(x+3y)k^
Step 2: Use the second condition to find a relationship between x and y.
The projection of vector v on vector c is given by the formula: Projcv=∣c∣v⋅c
First, calculate the magnitude of c: ∣c∣=(1)2+(−2)2+(1)2=1+4+1=6
Next, calculate the dot product v⋅c: v⋅c=((x+2y)i^+(x−y)j^+(x+3y)k^)⋅(i^−2j^+k^) v⋅c=(x+2y)(1)+(x−y)(−2)+(x+3y)(1) v⋅c=x+2y−2x+2y+x+3y v⋅c=(x−2x+x)+(2y+2y+3y) v⋅c=0x+7y=7y
Now, substitute these into the projection formula and set it equal to the given value: 67y=61 Multiplying both sides by 6, we get: 7y=1⟹y=71
Step 3: Substitute the value of y back into the expression for v. v=xa+71b v=x(i^+j^+k^)+71(2i^−j^+3k^) v=(x+72)i^+(x−71)j^+(x+73)k^
Step 4: Check the given options to find the correct value of x.
We need to find which of the given options matches this form of v for a consistent value of x.
Let's test Option 4: v=71(9i^+6j^+10k^)=79i^+76j^+710k^ Equating the components with our derived form of v:
For the i^ component: x+72=79⟹x=79−72=77=1 For the j^ component: x−71=76⟹x=76+71=77=1 For the k^ component: x+73=710⟹x=710−73=77=1
Since all three components yield a consistent value of x=1, Option 4 is the correct vector. The vector is v=1⋅a+71⋅b. This vector inherently lies in the plane of a and b by its construction.
Let's verify the vector v=a+71b: v=(i^+j^+k^)+71(2i^−j^+3k^) v=i^+j^+k^+72i^−71j^+73k^ v=(1+72)i^+(1−71)j^+(1+73)k^ v=79i^+76j^+710k^=71(9i^+6j^+10k^)
This confirms that Option 4 is the correct vector.
