Question
Question: The centre of mass of given system is at a distance x from geometrical centre of bigger body....
The centre of mass of given system is at a distance x from geometrical centre of bigger body.
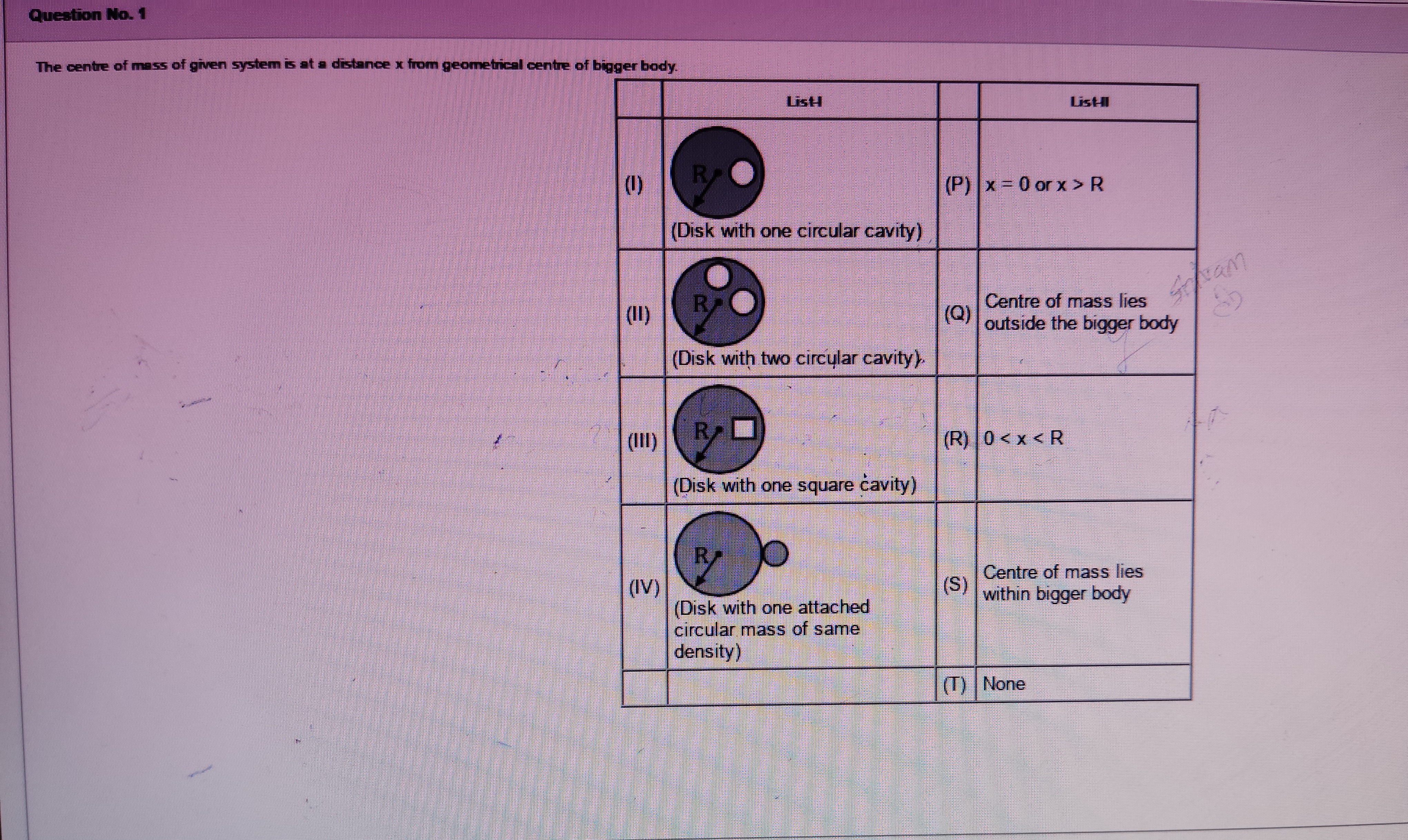
x = 0 or x > R
Centre of mass lies outside the bigger body
0 < x < R
Centre of mass lies within bigger body
None
0 < x < R
Solution
The center of mass of a system can be calculated using the formula RCM=∑mi∑miri. For a continuous body with mass density ρ(r), the formula is RCM=∫dm∫rdm=∫ρ(r)dV∫rρ(r)dV.
When dealing with a body with a cavity, we can use the concept of negative mass. The system is treated as a complete body of positive mass minus the mass of the cavity. If the density is uniform, ρ=σ (mass per unit area for a thin disk).
Let the geometrical center of the bigger disk be the origin (0, 0). The radius of the bigger disk is R.
(I) Disk with one circular cavity: A circular cavity of radius r is removed, with its center at a distance d from the origin. The figure shows the cavity is off-center, so d>0. The cavity is inside the disk, so d+r≤R. Mass of the complete disk M=σπR2. Its center of mass is at (0, 0). Mass of the cavity m=σπr2. Its center of mass is at a position d from the origin, with ∣d∣=d. The center of mass of the system with the cavity is XCM=M−mM⋅0−md=M−m−md. The distance of the center of mass from the origin is x=∣XCM∣=M−mmd=σπR2−σπr2σπr2d=R2−r2r2d. Since the cavity is off-center, d>0, so x>0. Since the cavity is inside the disk, d≤R−r. So x≤R2−r2r2(R−r)=(R−r)(R+r)r2(R−r)=R+rr2. Since r<R, R+r>2r, so R+rr2<2rr2=2r. Also r<R. So x<R. Thus, for case (I), 0<x<R. This corresponds to option (R). Since x<R, the center of mass is within the bigger body, so it also corresponds to option (S). However, (R) is a more specific range for x.
