Question

The velocity-time graph of a body is shown in figure. The ratio of the ...during the intervals OA and AB is....

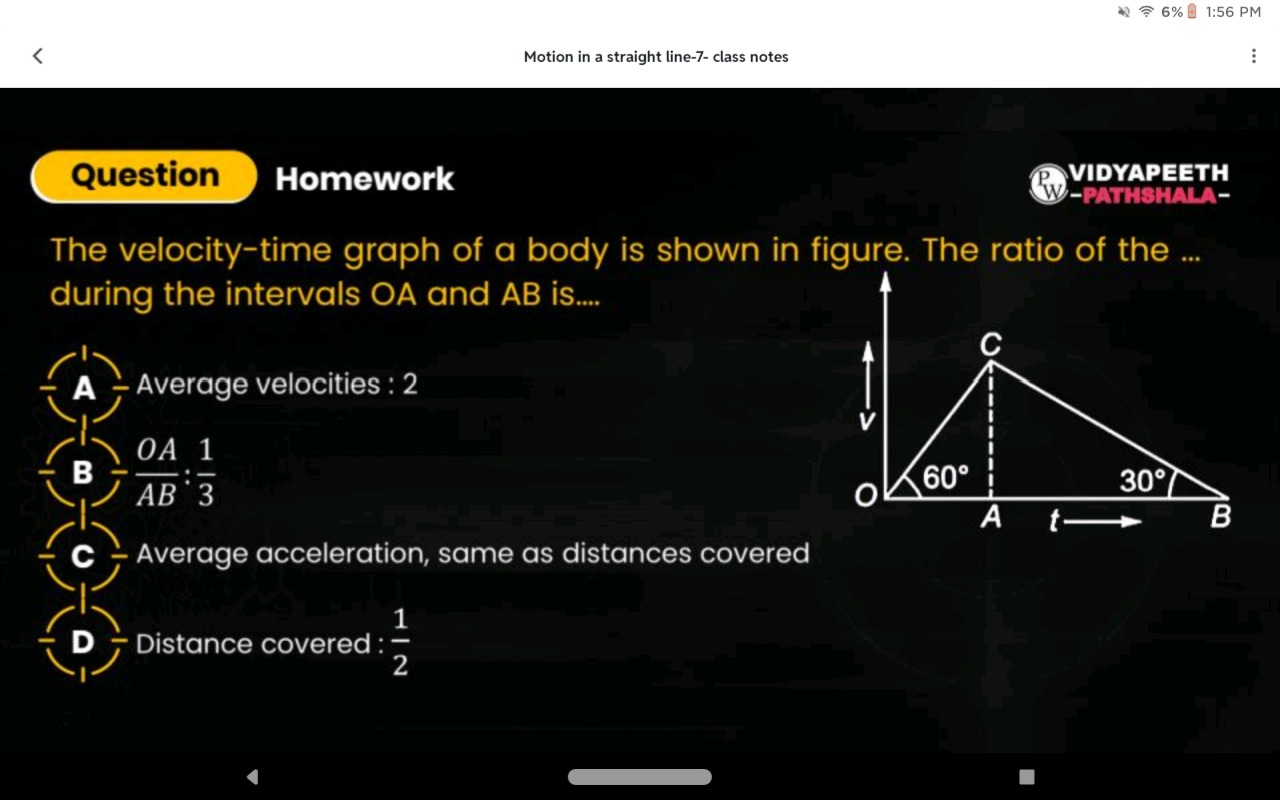
• A. Average velocities : 2
• B. $\frac{OA}{AB}$:$\frac{1}{3}$
• C. Average acceleration, same as distances covered
• D. Distance covered: $\frac{1}{2}$

Answer 1

Answer: (B)

$\frac{OA}{AB}$:$\frac{1}{3}$

Answer 2

The problem asks for the ratio of a certain physical quantity during the intervals OA and AB, based on the provided velocity-time (v-t) graph. The specific quantity is not mentioned in the question prompt but can be inferred from the options.

Let $V_C$ be the maximum velocity attained at point C, and let $t_A$ be the time corresponding to point A. The time duration for interval OA is $t_{OA} = t_A$. The time duration for interval AB is $t_{AB} = t_B - t_A$.

1. Analyze Interval OA:

The graph for interval OA is a straight line starting from the origin (0,0) and ending at $(t_A, V_C)$.

The slope of the v-t graph represents acceleration.

The angle the line OA makes with the time axis is $60^\circ$.

So, the acceleration during OA is $a_{OA} = \tan(60^\circ) = \sqrt{3}$.

Also, $a_{OA} = \frac{V_C - 0}{t_A - 0} = \frac{V_C}{t_A}$.

From this, we get $V_C = \sqrt{3} t_A$. (Equation 1)

2. Analyze Interval AB:

The graph for interval AB is a straight line starting from $(t_A, V_C)$ and ending at $(t_B, 0)$.

The angle the line CB makes with the time axis is $30^\circ$. The slope is negative as velocity is decreasing.

The magnitude of acceleration (deceleration) during AB is $|a_{AB}| = \tan(30^\circ) = \frac{1}{\sqrt{3}}$.

Also, $a_{AB} = \frac{0 - V_C}{t_B - t_A} = -\frac{V_C}{t_{AB}}$.

So, $|a_{AB}| = \frac{V_C}{t_{AB}} = \frac{1}{\sqrt{3}}$.

From this, we get $V_C = \frac{1}{\sqrt{3}} t_{AB}$. (Equation 2)

3. Compare Time Durations (from Option B):

From Equation 1 and Equation 2, we can equate the expressions for $V_C$:

$\sqrt{3} t_A = \frac{1}{\sqrt{3}} t_{AB}$

Multiplying both sides by $\sqrt{3}$:

$3 t_A = t_{AB}$

The ratio of time durations $\frac{t_{OA}}{t_{AB}} = \frac{t_A}{t_{AB}} = \frac{1}{3}$.

Option B states "$\frac{OA}{AB}:\frac{1}{3}$". Since OA and AB represent the time intervals on the graph, this option refers to the ratio of time durations, which is $1/3$. So, option B is consistent with our calculation.

4. Check other quantities:

a) Average Velocities (from Option A):

Average velocity for uniform acceleration/deceleration is (initial velocity + final velocity) / 2.

Average velocity for OA: $V_{avg, OA} = \frac{0 + V_C}{2} = \frac{V_C}{2}$.

Average velocity for AB: $V_{avg, AB} = \frac{V_C + 0}{2} = \frac{V_C}{2}$.

The ratio of average velocities $\frac{V_{avg, OA}}{V_{avg, AB}} = \frac{V_C/2}{V_C/2} = 1$.

Option A states "Average velocities : 2", which is incorrect.

b) Distances Covered (from Option D):

Distance covered is the area under the v-t graph.

Distance covered in OA: $d_{OA} = \text{Area of triangle OAC} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times t_A \times V_C$.

Distance covered in AB: $d_{AB} = \text{Area of triangle ABC} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times t_{AB} \times V_C$.

The ratio of distances covered $\frac{d_{OA}}{d_{AB}} = \frac{\frac{1}{2} t_A V_C}{\frac{1}{2} t_{AB} V_C} = \frac{t_A}{t_{AB}}$.

Since we found $\frac{t_A}{t_{AB}} = \frac{1}{3}$, the ratio of distances covered is also $\frac{1}{3}$.

Option D states "Distance covered: $\frac{1}{2}$", which is incorrect.

c) Average Acceleration (from Option C):

Magnitude of average acceleration for OA: $|a_{OA}| = \sqrt{3}$.

Magnitude of average acceleration for AB: $|a_{AB}| = \frac{1}{\sqrt{3}}$.

Ratio of magnitudes of average accelerations $\frac{|a_{OA}|}{|a_{AB}|} = \frac{\sqrt{3}}{1/\sqrt{3}} = 3$.

Option C states "Average acceleration, same as distances covered". The ratio of average accelerations (3) is not the same as the ratio of distances covered (1/3). So, option C is incorrect.

Based on the analysis, option B is the only correct statement, indicating that the ratio of the time durations (or distances covered, as both yield 1/3) for intervals OA and AB is 1/3. Given the notation "OA/AB", it most directly refers to the ratio of time durations.