Question
Question: If $y = (\tan^{-1}x)^2$ then $(x^2 + 1)^2\frac{d^2y}{dx^2} + 2x(x^2 + 1)\frac{dy}{dx} =$...
If y=(tan−1x)2 then (x2+1)2dx2d2y+2x(x2+1)dxdy=
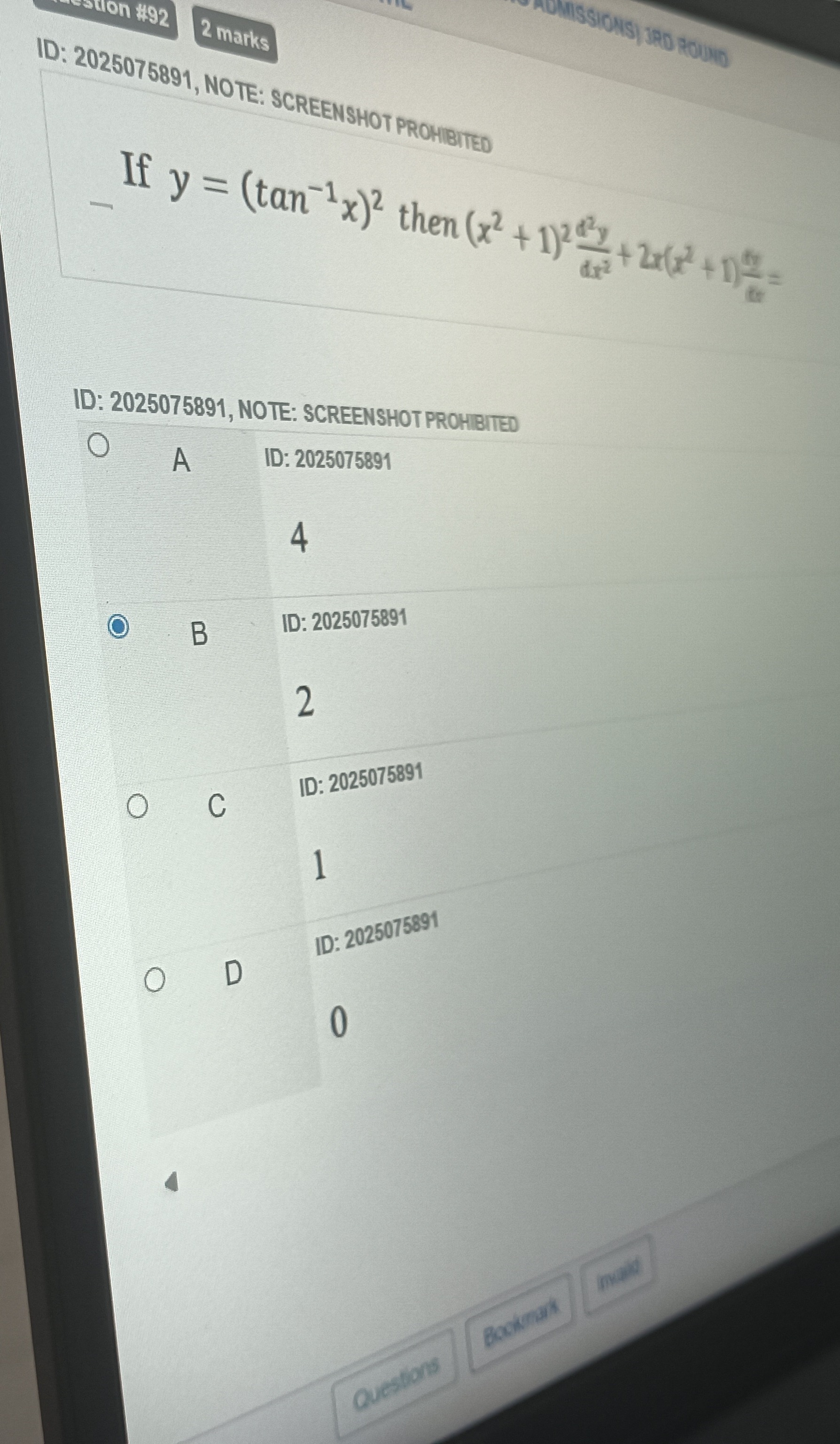
4
2
1
0
2
Solution
The problem asks us to find the value of the expression (x2+1)2dx2d2y+2x(x2+1)dxdy given that y=(tan−1x)2.
Step 1: Find the first derivative dxdy. Given y=(tan−1x)2. Using the chain rule, dxdy=2(tan−1x)⋅dxd(tan−1x). We know that dxd(tan−1x)=1+x21. So, dxdy=2(tan−1x)⋅1+x21 Rearrange this equation by multiplying both sides by (1+x2): (1+x2)dxdy=2tan−1x(Equation 1)
Step 2: Find the second derivative dx2d2y. Differentiate both sides of Equation 1 with respect to x. For the left side, use the product rule dxd(uv)=u′v+uv′ where u=(1+x2) and v=dxdy. dxd((1+x2)dxdy)=dxd(1+x2)⋅dxdy+(1+x2)⋅dxd(dxdy) =2xdxdy+(1+x2)dx2d2y For the right side, differentiate 2tan−1x: dxd(2tan−1x)=2⋅1+x21 Equating the derivatives of both sides: 2xdxdy+(1+x2)dx2d2y=1+x22(Equation 2)
Step 3: Obtain the required expression. The expression we need to find is (x2+1)2dx2d2y+2x(x2+1)dxdy. Notice that if we multiply Equation 2 by (1+x2), we will get the required expression. Multiply both sides of Equation 2 by (1+x2): (1+x2)[2xdxdy+(1+x2)dx2d2y]=(1+x2)[1+x22] Distribute (1+x2) on the left side: 2x(1+x2)dxdy+(1+x2)2dx2d2y=2 Rearranging the terms to match the question's format: (x2+1)2dx2d2y+2x(x2+1)dxdy=2
The value of the expression is 2.
