Question

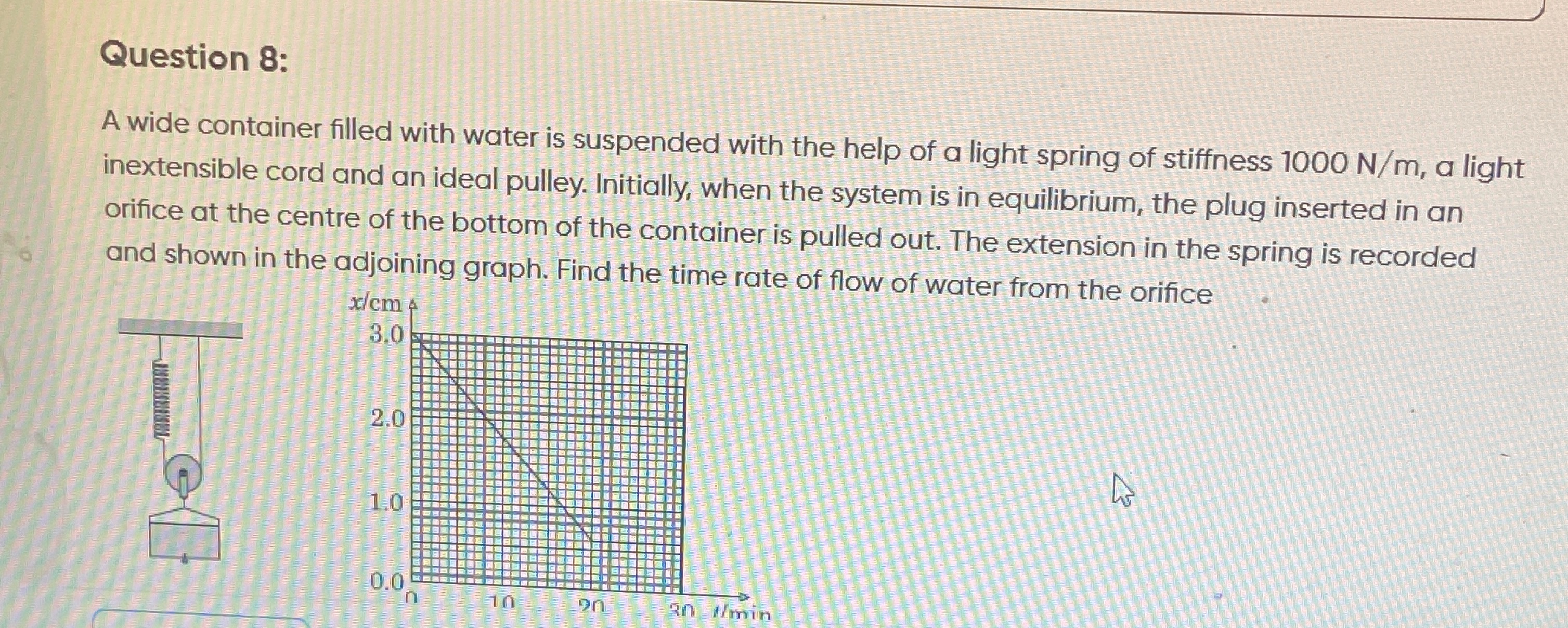
A wide container filled with water is suspended with the help of a light spring of stiffness 1000 N/m, a light inextensible cord and an ideal pulley. Initially, when the system is in equilibrium, the plug inserted in an orifice at the centre of the bottom of the container is pulled out. The extension in the spring is recorded and shown in the adjoining graph. Find the time rate of flow of water from the orifice

Answer 1

0.15 liters/min

Answer 2

The system consists of a container of water suspended by a spring. The extension of the spring, $x$, is related to the mass of water, $m$, by the equilibrium condition: $kx = mg$. The graph shows that the extension $x$ decreases linearly with time $t$. This implies that the mass of water $m$ also decreases linearly with time, meaning the rate of mass flow, $\frac{dm}{dt}$, is constant.

From the graph, at $t=0$, $x = 3.0$ cm. At $t=20$ minutes, $x = 0$ cm. The rate of change of extension is: $\frac{dx}{dt} = \frac{\Delta x}{\Delta t} = \frac{0 \text{ cm} - 3.0 \text{ cm}}{20 \text{ min} - 0 \text{ min}} = -0.15 \text{ cm/min}$.

From the equilibrium equation, $m = \frac{k}{g}x$. Differentiating with respect to time, we get: $\frac{dm}{dt} = \frac{k}{g}\frac{dx}{dt}$.

We are given $k = 1000$ N/m. Let's use $g = 10$ m/s$^2$. We need to ensure consistent units. Let's use SI units for $k$ and $g$, and convert $\frac{dx}{dt}$ to m/min. $\frac{dx}{dt} = -0.15 \frac{\text{cm}}{\text{min}} = -0.15 \times 10^{-2} \frac{\text{m}}{\text{min}}$.

Now, calculate the rate of mass flow: $\frac{dm}{dt} = \frac{1000 \text{ N/m}}{10 \text{ m/s}^2} \times (-0.15 \times 10^{-2} \text{ m/min})$ $\frac{dm}{dt} = 100 \text{ kg/m} \times (-0.15 \times 10^{-2} \text{ m/min})$ $\frac{dm}{dt} = -0.15 \text{ kg/min}$.

The question asks for the "time rate of flow of water", which usually refers to the volume flow rate, $Q = \frac{dV}{dt}$. The relationship between mass and volume is $m = \rho V$, where $\rho$ is the density of water. Assuming $\rho = 1000$ kg/m$^3$. $Q = \frac{dm}{dt} / \rho = \frac{-0.15 \text{ kg/min}}{1000 \text{ kg/m}^3} = -0.15 \times 10^{-3} \text{ m}^3/\text{min}$.

The question does not specify units for the answer, but typical units for flow rate are liters per minute or m$^3$/s. Let's convert to liters per minute. $1$ m$^3 = 1000$ liters. $Q = -0.15 \times 10^{-3} \frac{\text{m}^3}{\text{min}} \times \frac{1000 \text{ liters}}{1 \text{ m}^3} = -0.15 \text{ liters/min}$. The rate of flow is the magnitude of this value, so $|Q| = 0.15$ liters/min.