Question
Question: The angle between the lines $3x-4y=1$ and $2x+3y=5$ is...
The angle between the lines 3x−4y=1 and 2x+3y=5 is
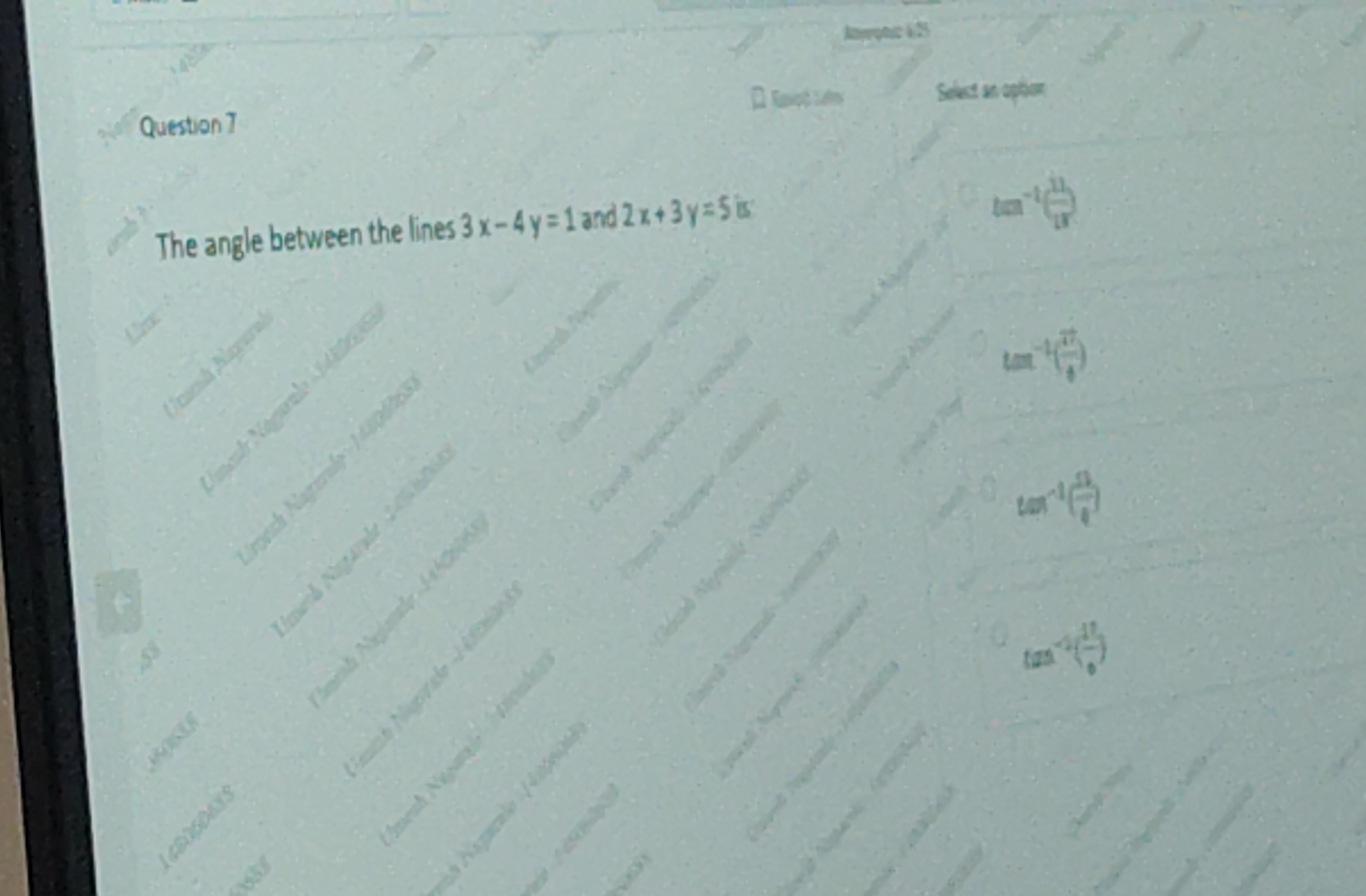
tan−1(6−17)
tan−1(6−1)
tan−1(61)
tan−1(617)
tan−1(617)
Solution
To find the angle between two lines, we first determine their slopes. The general equation of a straight line is Ax+By+C=0. Its slope m can be found by rearranging it into the slope-intercept form y=mx+c, where m=−BA.
Step 1: Find the slope of the first line. The equation of the first line is 3x−4y=1. Rearrange it to solve for y: 4y=3x−1 y=43x−41 So, the slope of the first line, m1=43.
Step 2: Find the slope of the second line. The equation of the second line is 2x+3y=5. Rearrange it to solve for y: 3y=−2x+5 y=−32x+35 So, the slope of the second line, m2=−32.
Step 3: Use the formula for the angle between two lines. The angle θ between two lines with slopes m1 and m2 is given by the formula: tanθ=1+m1m2m2−m1 This formula gives the acute angle between the lines.
Substitute the values of m1 and m2 into the formula: m1=43 m2=−32
Calculate the numerator m2−m1: m2−m1=−32−43=12−2×4−3×3=12−8−9=−1217
Calculate the denominator 1+m1m2: 1+m1m2=1+(43)(−32)=1−126=1−21=21
Now, substitute these values into the tanθ formula: tanθ=21−1217 tanθ=−1217×12 tanθ=−617 tanθ=617
Therefore, the angle θ is tan−1(617).
