Question
Question: Adjoint of the matrix $N = \begin{bmatrix} -4 & -3 & -3 \\ 1 & 0 & 1 \\ 4 & 4 & 3 \end{bmatrix}$ is...
Adjoint of the matrix
N=−414−304−313 is
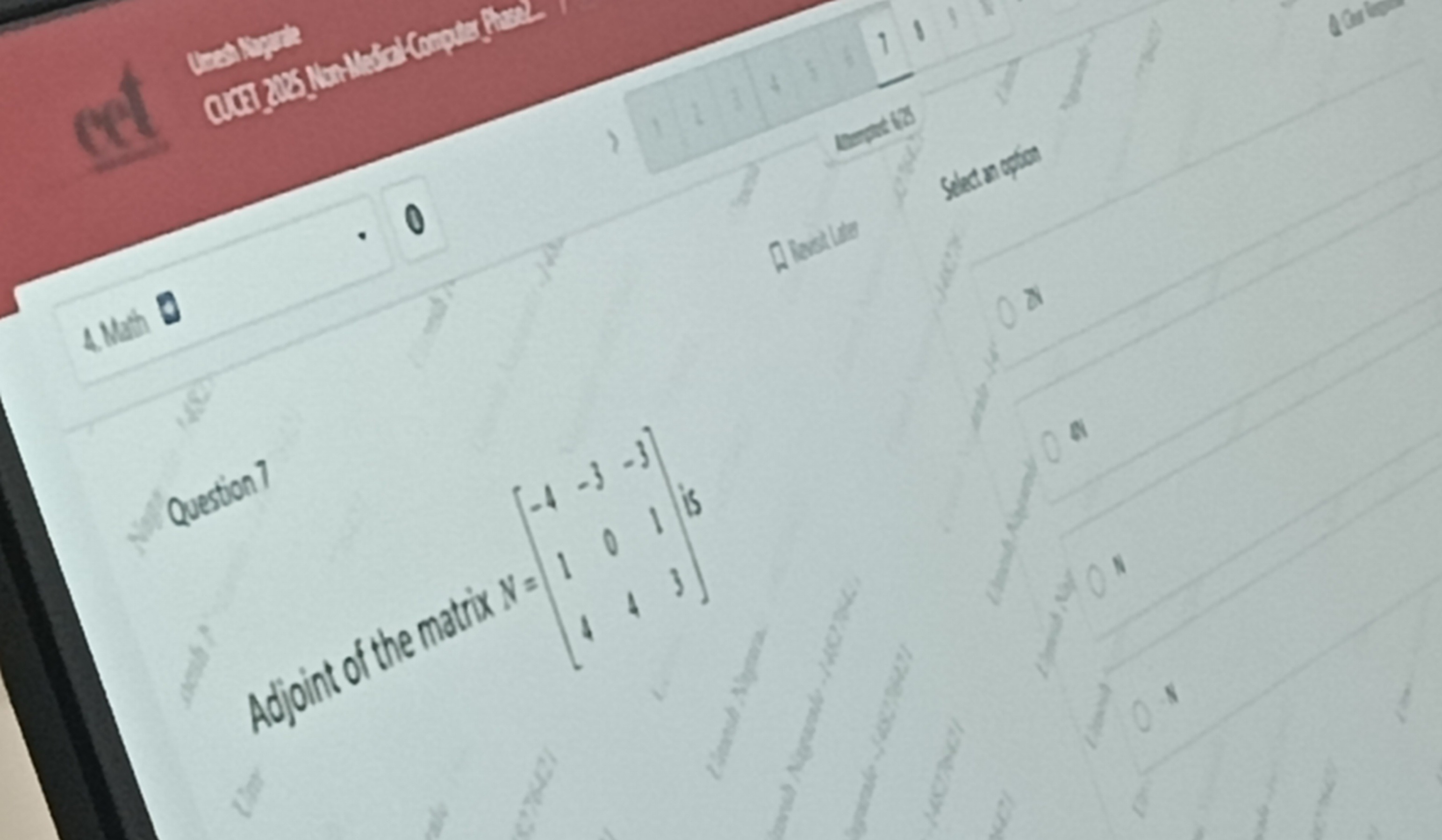
−414−304−313
−414−304−313
Solution
To find the adjoint of a matrix N, we follow these steps:
- Calculate the cofactor of each element of the matrix.
- Form the cofactor matrix.
- Take the transpose of the cofactor matrix to get the adjoint matrix.
Given matrix: N=−414−304−313
Step 1: Calculate the cofactors
The cofactor Cij of an element aij is given by Cij=(−1)i+jMij, where Mij is the minor of aij.
C11=(−1)1+10413=(0×3−1×4)=0−4=−4
C12=(−1)1+21413=−(1×3−1×4)=−(3−4)=−(−1)=1
C13=(−1)1+31404=(1×4−0×4)=4−0=4
C21=(−1)2+1−34−33=−((−3)×3−(−3)×4)=−(−9−(−12))=−(−9+12)=−(3)=−3
C22=(−1)2+2−44−33=(−4)×3−(−3)×4=−12−(−12)=−12+12=0
C23=(−1)2+3−44−34=−((−4)×4−(−3)×4)=−(−16−(−12))=−(−16+12)=−(−4)=4
C31=(−1)3+1−30−31=(−3)×1−(−3)×0=−3−0=−3
C32=(−1)3+2−41−31=−((−4)×1−(−3)×1)=−(−4−(−3))=−(−4+3)=−(−1)=1
C33=(−1)3+3−41−30=(−4)×0−(−3)×1=0−(−3)=3
Step 2: Form the cofactor matrix
The cofactor matrix C is: C=C11C21C31C12C22C32C13C23C33=−4−3−3101443
Step 3: Take the transpose of the cofactor matrix
The adjoint of N, denoted as adj(N), is CT: adj(N)=CT=−414−304−313
Notice that the calculated adjoint matrix is identical to the original matrix N. adj(N)=N
This implies that the matrix N is an involutory matrix (a matrix that is its own inverse, since N−1=det(N)1adj(N) and if adj(N)=N, then N−1=det(N)1N. For N−1=N, we must have det(N)=1). Let's verify the determinant of N: det(N)=−4(0×3−1×4)−(−3)(1×3−1×4)+(−3)(1×4−0×4) det(N)=−4(−4)+3(−1)−3(4) det(N)=16−3−12=1 Since det(N)=1, our result adj(N)=N is consistent with N−1=N.
The final answer is N
Explanation of the solution:
- Calculate all nine cofactors Cij for the given matrix N.
- Arrange these cofactors into a matrix, called the cofactor matrix.
- The adjoint of matrix N is the transpose of this cofactor matrix.
- After calculation, the adjoint matrix is found to be identical to the original matrix N.
Answer:
The adjoint of the matrix N is: adj(N)=−414−304−313=N
