Question

A charged particle of mass $m$ and charge $q$ is projected horizontally into uniform magnetic field of width $d$ and magnitude $B$. The particle leaves the region at angle $\theta=30^\circ$ with horizontal as shown. The value of $d$ is

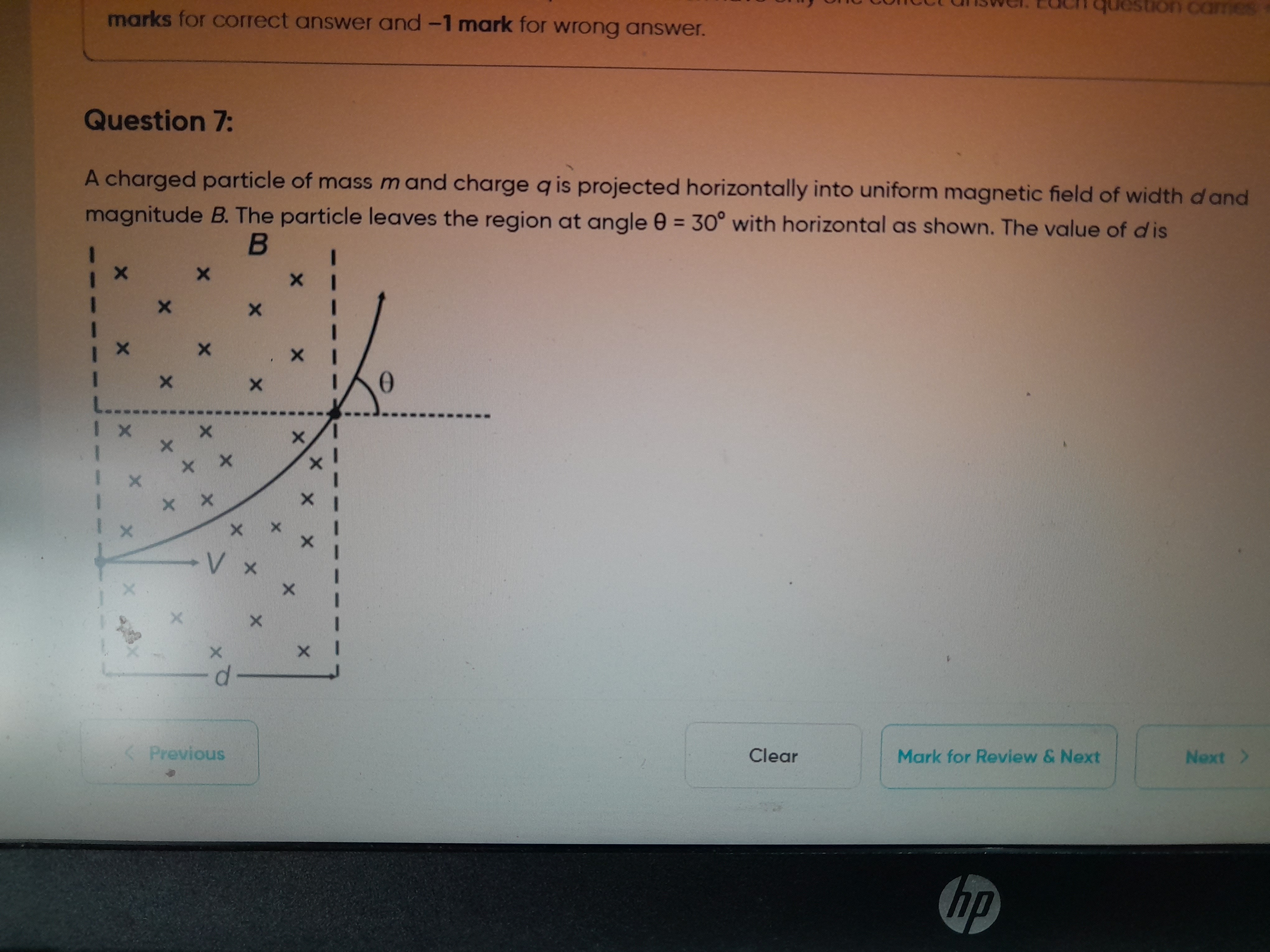
• A. $\frac{mV}{qB}$
• B. $\frac{mV}{2qB}$
• C. $\frac{2mV}{qB}$
• D. $\frac{3mV}{2qB}$

Answer 1

Answer: (B)

$\frac{mV}{2qB}$

Answer 2

The charged particle moves in a circular path of radius $R = \frac{mV}{qB}$ due to the magnetic force. The initial velocity is horizontal, and the magnetic field causes the particle to curve upwards. The angle $\theta$ at which the particle exits is the same as the angle subtended by the arc at the center of the circular path. From the geometry, the horizontal distance $d$ is related to the radius $R$ and the angle $\theta$ by $d = R \sin(\theta)$. Substituting the expression for $R$ and the given angle $\theta = 30^\circ$, we get $d = \frac{mV}{qB} \sin(30^\circ) = \frac{mV}{2qB}$.