Question

If the product of n matrices $\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}$ $\begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix}$ $\begin{bmatrix} 1 & 3 \\ 0 & 1 \end{bmatrix}$... $\begin{bmatrix} 1 & n \\ 0 & 1 \end{bmatrix}$ is equal to the matrix $\begin{bmatrix} 1 & 120 \\ 0 & 1 \end{bmatrix}$ then the value of n is equal to

Answer 1

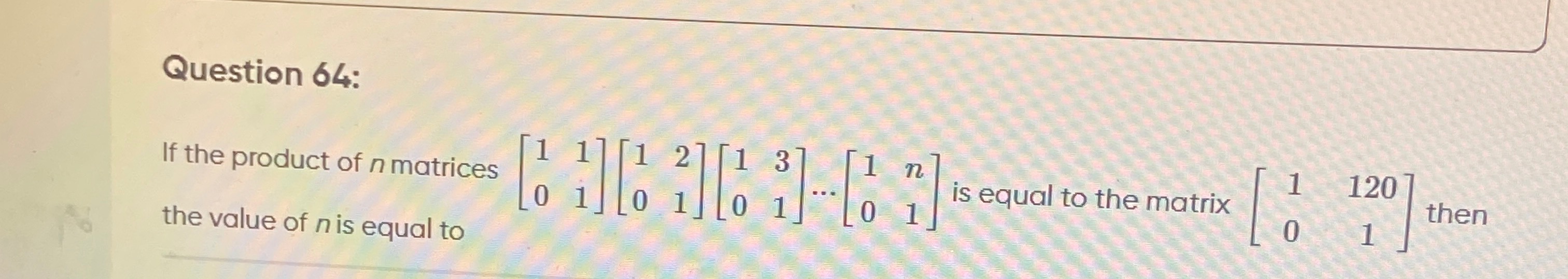
15

Answer 2

To find the value of 'n', we first need to determine the general form of the product of the given 'n' matrices.

Let the matrices be $M_k = \begin{bmatrix} 1 & k \\ 0 & 1 \end{bmatrix}$. We need to find the product $P_n = M_1 M_2 M_3 ... M_n$.

Let's multiply the first few matrices to observe a pattern:

1. Product of the first two matrices: $P_2 = M_1 M_2 = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix}$ $P_2 = \begin{bmatrix} (1)(1) + (1)(0) & (1)(2) + (1)(1) \\ (0)(1) + (1)(0) & (0)(2) + (1)(1) \end{bmatrix}$ $P_2 = \begin{bmatrix} 1 & 2+1 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 3 \\ 0 & 1 \end{bmatrix}$

2. Product of the first three matrices: $P_3 = P_2 M_3 = \begin{bmatrix} 1 & 3 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 3 \\ 0 & 1 \end{bmatrix}$ $P_3 = \begin{bmatrix} (1)(1) + (3)(0) & (1)(3) + (3)(1) \\ (0)(1) + (1)(0) & (0)(3) + (1)(1) \end{bmatrix}$ $P_3 = \begin{bmatrix} 1 & 3+3 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 6 \\ 0 & 1 \end{bmatrix}$

From these calculations, we observe a pattern: The product of matrices of the form $\begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix}$ and $\begin{bmatrix} 1 & b \\ 0 & 1 \end{bmatrix}$ is $\begin{bmatrix} 1 & a+b \\ 0 & 1 \end{bmatrix}$. Applying this rule iteratively, the product of 'n' matrices $\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}$, $\begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix}$, ..., $\begin{bmatrix} 1 & n \\ 0 & 1 \end{bmatrix}$ will result in a matrix where the top-left element is 1, the bottom-left element is 0, the bottom-right element is 1, and the top-right element is the sum of the numbers 1, 2, ..., n.

The sum of the first 'n' natural numbers is given by the formula $S_n = \frac{n(n+1)}{2}$.

Therefore, the product of the 'n' matrices is: $P_n = \begin{bmatrix} 1 & 1+2+3+...+n \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & \frac{n(n+1)}{2} \\ 0 & 1 \end{bmatrix}$

We are given that this product is equal to the matrix $\begin{bmatrix} 1 & 120 \\ 0 & 1 \end{bmatrix}$. By comparing the elements of the two matrices, we can equate the top-right elements: $\frac{n(n+1)}{2} = 120$

Now, we solve for 'n': $n(n+1) = 120 \times 2$ $n(n+1) = 240$

We need to find an integer 'n' such that the product of 'n' and 'n+1' is 240. We can either test integer values or solve the quadratic equation $n^2 + n - 240 = 0$.

By observation: We know that $15 \times 16 = 240$. So, if $n=15$, then $n+1=16$, and $n(n+1) = 15 \times 16 = 240$. This matches the equation.

Alternatively, solving the quadratic equation: $n^2 + n - 240 = 0$ Using the quadratic formula $n = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$: $n = \frac{-1 \pm \sqrt{1^2 - 4(1)(-240)}}{2(1)}$ $n = \frac{-1 \pm \sqrt{1 + 960}}{2}$ $n = \frac{-1 \pm \sqrt{961}}{2}$ Since $31^2 = 961$, we have $\sqrt{961} = 31$. $n = \frac{-1 \pm 31}{2}$

Two possible solutions for 'n': $n_1 = \frac{-1 + 31}{2} = \frac{30}{2} = 15$ $n_2 = \frac{-1 - 31}{2} = \frac{-32}{2} = -16$

Since 'n' represents the number of matrices, it must be a positive integer. Therefore, $n=15$.