Solveeit Logo
Login

Question

Question: A string of length 1 m is fixed at one end and carries a mass 100 g at the other end. The string mak...

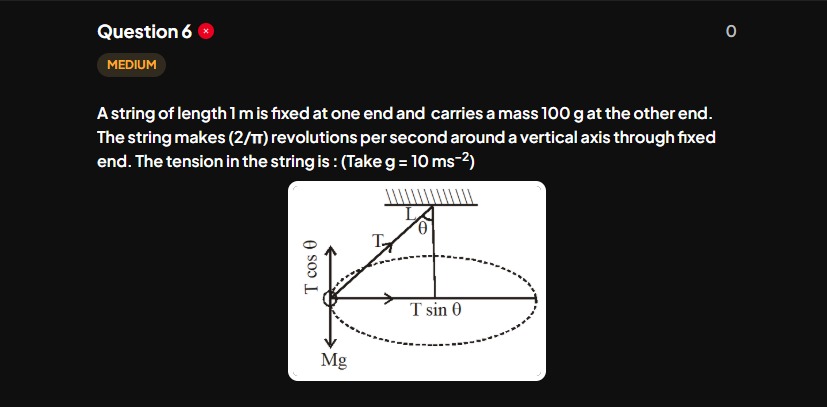
A string of length 1 m is fixed at one end and carries a mass 100 g at the other end. The string makes (2/ㅠ) revolutions per second around a vertical axis through fixed end. The tension in the string is : (Take g = 10 ms⁻²)

A

0.4 N

B

0.8 N

C

1.2 N

D

1.6 N

Answer

1.6 N

Explanation

Solution

The problem describes a conical pendulum. A mass 'm' is attached to a string of length 'L' and revolves around a vertical axis.

1. Identify the given parameters:

  • Length of the string, L=1 mL = 1 \text{ m}
  • Mass, m=100 g=0.1 kgm = 100 \text{ g} = 0.1 \text{ kg}
  • Frequency of revolution, f=2π revolutions per secondf = \frac{2}{\pi} \text{ revolutions per second}
  • Acceleration due to gravity, g=10 m/s2g = 10 \text{ m/s}^2

2. Calculate the angular velocity (ω\omega): The angular velocity is related to the frequency by the formula ω=2πf\omega = 2\pi f. ω=2π(2π) rad/s\omega = 2\pi \left(\frac{2}{\pi}\right) \text{ rad/s} ω=4 rad/s\omega = 4 \text{ rad/s}

3. Analyze the forces acting on the mass: When the mass revolves, it forms a conical pendulum. Let θ\theta be the angle the string makes with the vertical. The forces acting on the mass are:

  • Tension (T) along the string, directed towards the fixed support.
  • Weight (mg) acting vertically downwards.

4. Resolve the forces:

  • Vertical equilibrium: The vertical component of the tension balances the weight of the mass. Tcos⁡θ=mg…(1)T \cos \theta = mg \quad \dots(1)
  • Horizontal force (Centripetal force): The horizontal component of the tension provides the necessary centripetal force for circular motion. Tsin⁡θ=mv2r=mω2r…(2)T \sin \theta = \frac{mv^2}{r} = m\omega^2 r \quad \dots(2) Where 'r' is the radius of the horizontal circle. From the geometry of the conical pendulum, r=Lsin⁡θr = L \sin \theta.

5. Substitute 'r' into the centripetal force equation: Substituting r=Lsin⁡θr = L \sin \theta into equation (2): Tsin⁡θ=mω2(Lsin⁡θ)T \sin \theta = m\omega^2 (L \sin \theta)

6. Solve for Tension (T): Since the string is revolving and forming a conical pendulum, θ≠0\theta \neq 0, which means sin⁡θ≠0\sin \theta \neq 0. Therefore, we can cancel sin⁡θ\sin \theta from both sides of the equation: T=mω2LT = m\omega^2 L

7. Substitute the numerical values: T=(0.1 kg)(4 rad/s)2(1 m)T = (0.1 \text{ kg}) (4 \text{ rad/s})^2 (1 \text{ m}) T=0.1×16×1T = 0.1 \times 16 \times 1 T=1.6 NT = 1.6 \text{ N}

Verification (Optional - using vertical equilibrium): We can also find cos⁡θ\cos \theta from Tcos⁡θ=mgT \cos \theta = mg: cos⁡θ=mgT=0.1×101.6=11.6=1016=58\cos \theta = \frac{mg}{T} = \frac{0.1 \times 10}{1.6} = \frac{1}{1.6} = \frac{10}{16} = \frac{5}{8} Also, from the derivation of conical pendulum, cos⁡θ=gω2L\cos \theta = \frac{g}{\omega^2 L}. cos⁡θ=10(4)2×1=1016=58\cos \theta = \frac{10}{(4)^2 \times 1} = \frac{10}{16} = \frac{5}{8} Both methods are consistent, confirming the value of tension.

The final answer is 1.6 N\boxed{\text{1.6 N}}.

Explanation of the solution: The tension in a conical pendulum is determined by the horizontal component providing the centripetal force. Given the angular frequency ω=2πf=4 rad/s\omega = 2\pi f = 4 \text{ rad/s}, mass m=0.1 kgm = 0.1 \text{ kg}, and string length L=1 mL = 1 \text{ m}, the tension is T=mω2LT = m\omega^2 L. Substituting the values, T=(0.1)(42)(1)=1.6 NT = (0.1)(4^2)(1) = 1.6 \text{ N}.