Question

If two sets A and B are having 101 elements in common, then the number of elements common to each of the sets A×B and B×A are

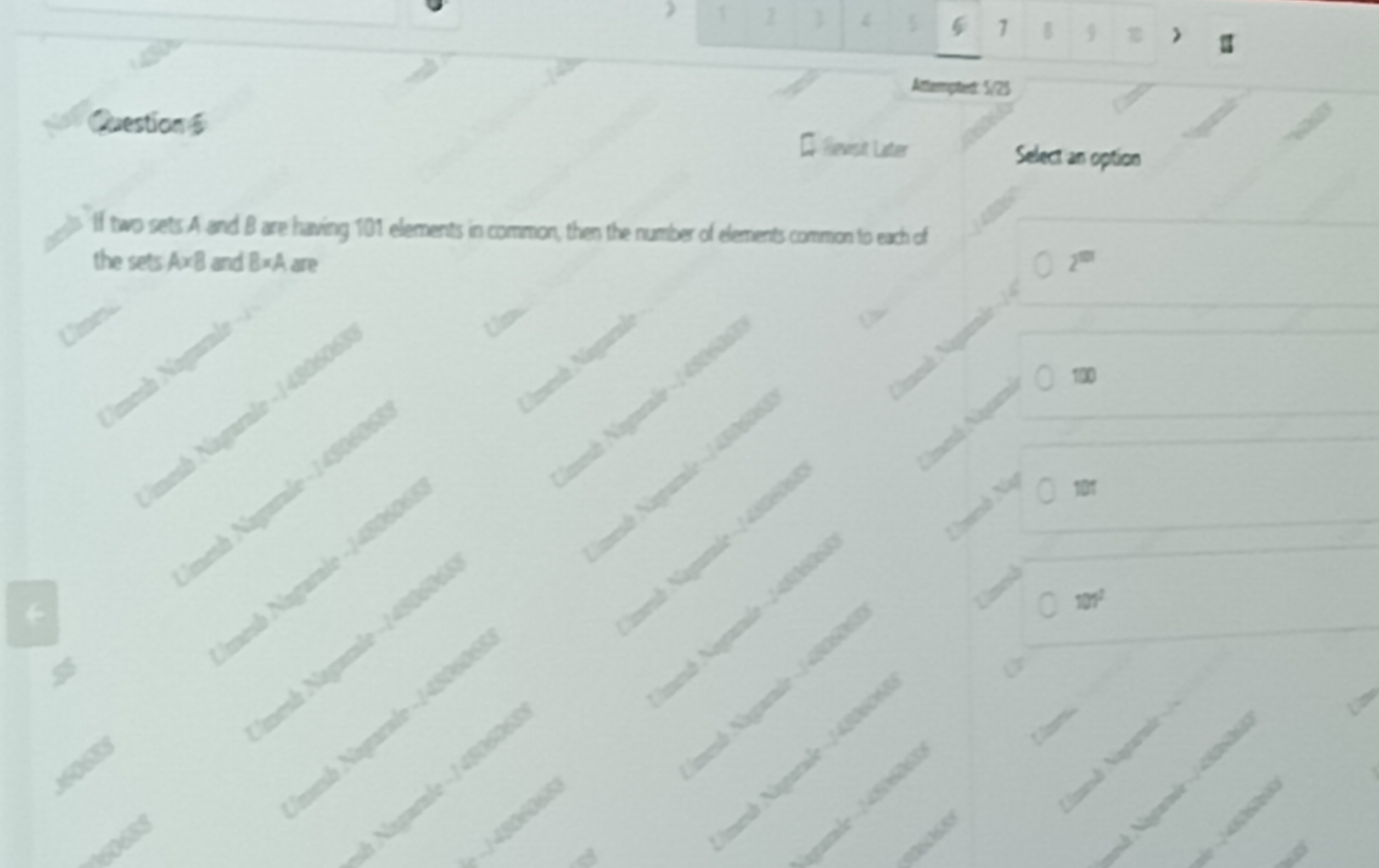
• A. $2^{101}$
• B. 100
• C. 101
• D. $101^2$

Answer 1

Answer: (D)

$101^2$

Answer 2

To find the number of elements common to both A×B and B×A, we need to determine the conditions under which an ordered pair (x, y) belongs to both sets.

Let (x, y) be an element in the intersection (A×B) ∩ (B×A).

For (x, y) to be in A×B, it must satisfy: x ∈ A and y ∈ B (Condition 1)

For (x, y) to be in B×A, it must satisfy: x ∈ B and y ∈ A (Condition 2)

For (x, y) to be common to both sets, both Condition 1 and Condition 2 must be true simultaneously.

From Condition 1 and Condition 2 for x: x ∈ A and x ∈ B This implies x ∈ A ∩ B.

From Condition 1 and Condition 2 for y: y ∈ B and y ∈ A This implies y ∈ B ∩ A.

Since A ∩ B = B ∩ A, we can say that for an element (x, y) to be in (A×B) ∩ (B×A), both x and y must belong to the set (A ∩ B).

Let C = A ∩ B. The problem states that A and B have 101 elements in common, so |A ∩ B| = 101. Therefore, |C| = 101.

The elements common to A×B and B×A are precisely the ordered pairs (x, y) such that x ∈ C and y ∈ C. This set of common elements is equivalent to the Cartesian product C × C.

The number of elements in C × C is given by |C| × |C|. Substituting the value of |C|: Number of common elements = 101 × 101 = $101^2$.