Question
Question: Anti muonic atom is with anti-muon (200 times massive to electron and having -ve electronic charge) ...
Anti muonic atom is with anti-muon (200 times massive to electron and having -ve electronic charge) and a positron. Ground state energy of hydrogen atom is -13.6 eV. The energy of atom in 9th excited state in anti-muonic atom is-
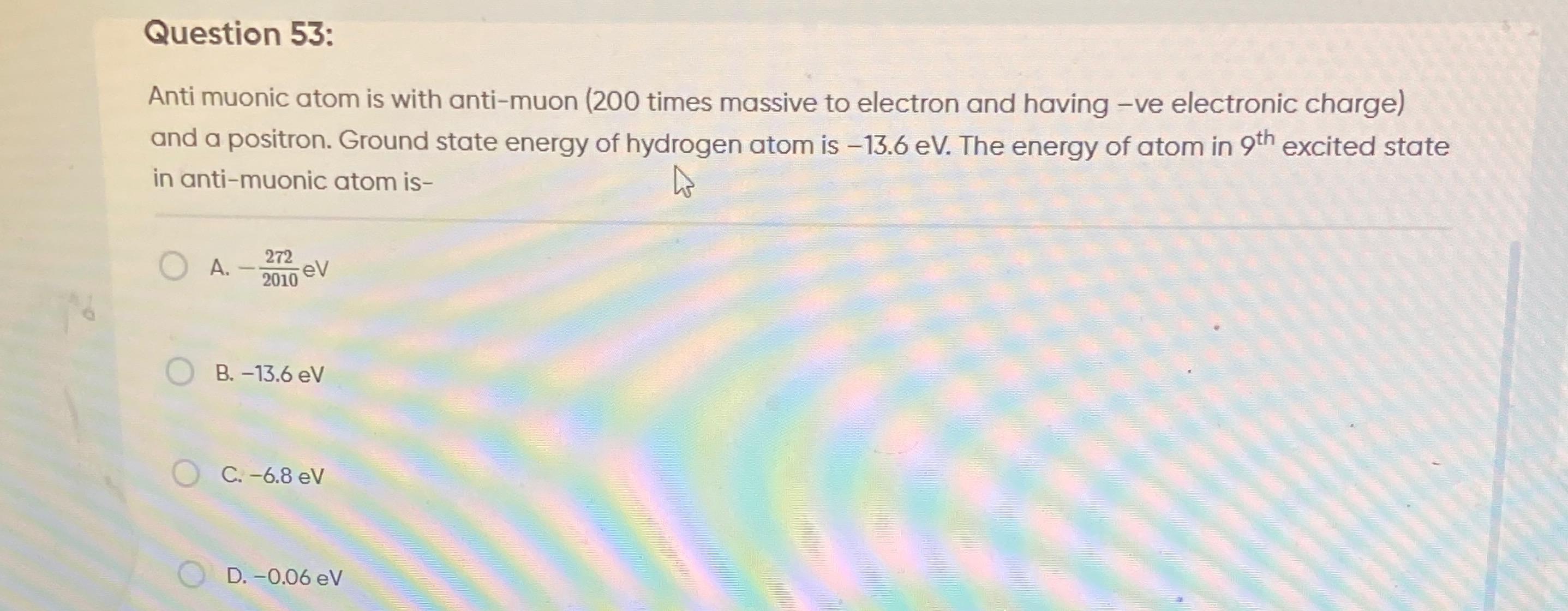
-2010272 eV
-13.6 eV
-6.8 eV
-0.06 eV
A
Solution
The energy levels of a hydrogen-like atom are given by En=−2ℏ2n2Z2μk2e4. For hydrogen, the ground state energy (n=1) is E1,H≈−2ℏ2mek2e4=−13.6 eV.
For the anti-muonic atom, the anti-muon has mass maμ=200me and the positron has mass mp=me. The reduced mass is μanti−μ=me+200meme(200me)=201200me.
The energy levels can be expressed as En≈meμanti−μ(n2−13.6 eV). The 9th excited state corresponds to n=10. E10≈me201200me(102−13.6 eV)=201200(100−13.6 eV)=20100200(−13.6 eV)=2012(−13.6 eV)=−20127.2 eV. This value is equivalent to -2010272 eV.
