Question

For the circuit shown below the capacitive reactance is $R$ and inductive reactance is $\sqrt{3}R$. The source voltage is $V=V_0 sin(\omega t)$. The phase difference between current though capacitor and inductor is $15N^{\circ}$. Find the value of $N$.

Answer 1

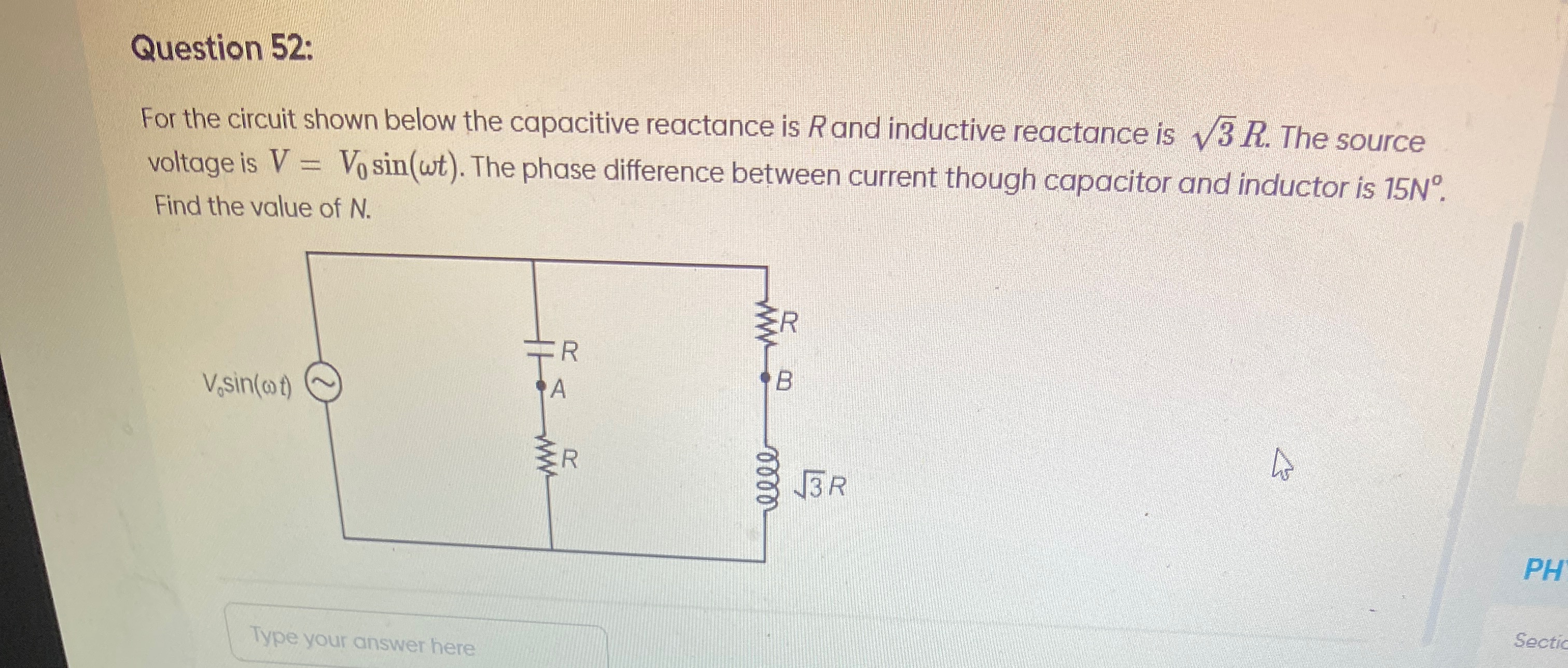
7

Answer 2

The circuit consists of two parallel branches connected to an AC voltage source $V = V_0 \sin(\omega t)$. Since the branches are in parallel, the voltage across each branch is the same as the source voltage. We can consider the source voltage as the reference phasor, i.e., $V = V_0 \angle 0^\circ$.

Branch 1 (Capacitor and Resistor in series): This branch contains a capacitor with capacitive reactance $X_C = R$ and a resistor with resistance $R_1 = R$. The impedance of this branch is $Z_1 = R_1 - jX_C = R - jR$. To find the phase of the current in this branch ($I_C$) relative to the voltage, we determine the phase angle of $Z_1$. The phase angle $\phi_1$ of $Z_1$ is given by: $\phi_1 = \arctan\left(\frac{-X_C}{R_1}\right) = \arctan\left(\frac{-R}{R}\right) = \arctan(-1) = -45^\circ$ Since the current in a series AC circuit is given by $I = V/Z$, the phase of the current $I_C$ will be $0^\circ - \phi_1$. Therefore, the phase of the current through the capacitor (and the entire Branch 1) is $\theta_C = 0^\circ - (-45^\circ) = +45^\circ$. This means the current $I_C$ leads the voltage $V$ by $45^\circ$.

Branch 2 (Resistor and Inductor in series): This branch contains a resistor with resistance $R_2 = R$ and an inductor with inductive reactance $X_L = \sqrt{3}R$. The impedance of this branch is $Z_2 = R_2 + jX_L = R + j\sqrt{3}R$. To find the phase of the current in this branch ($I_L$) relative to the voltage, we determine the phase angle of $Z_2$. The phase angle $\phi_2$ of $Z_2$ is given by: $\phi_2 = \arctan\left(\frac{X_L}{R_2}\right) = \arctan\left(\frac{\sqrt{3}R}{R}\right) = \arctan(\sqrt{3}) = +60^\circ$ The phase of the current through the inductor (and the entire Branch 2) is $\theta_L = 0^\circ - \phi_2$. Therefore, $\theta_L = 0^\circ - 60^\circ = -60^\circ$. This means the current $I_L$ lags the voltage $V$ by $60^\circ$.

Phase Difference between Currents: The phase difference between the current through the capacitor ($I_C$) and the current through the inductor ($I_L$) is the absolute difference between their phase angles: $\Delta\phi = |\theta_C - \theta_L| = |45^\circ - (-60^\circ)| = |45^\circ + 60^\circ| = 105^\circ$

Finding the value of N: The problem states that the phase difference is $15N^\circ$. $15N^\circ = 105^\circ$ $N = \frac{105}{15}$ $N = 7$