Question

A streamline curvilinear flow exhibits circular curvature on a horizontal plane as shown in figure. At radius of curvature $r_1$ the velocity of stream is $v_1$ and pressure $p_1$ and another radius of curvature $r_2$ the velocity of stream is $v_2$ and pressure $p_2$. Choose the correct options

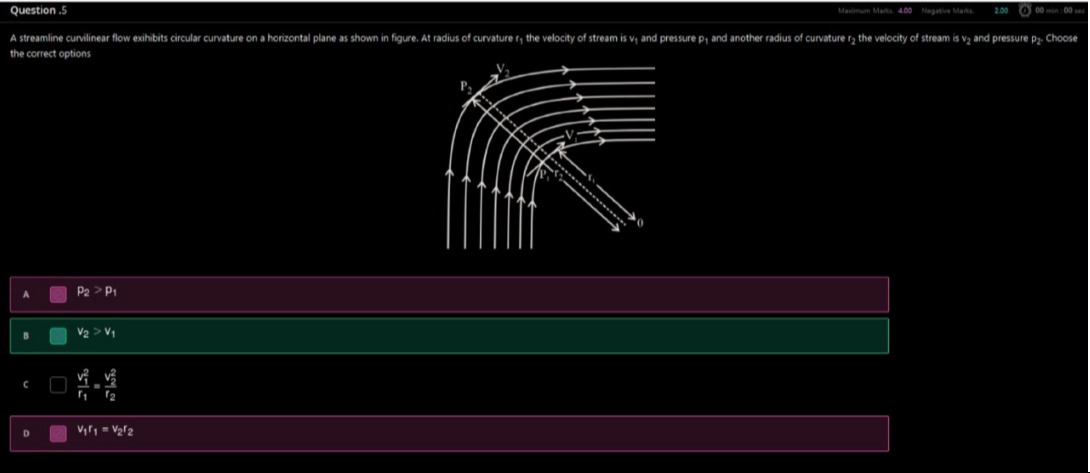
• A. p_2 > p_1
• B. v_2 > v_1
• C. $\frac{v_1^2}{r_1} = \frac{v_2^2}{r_2}$
• D. $v_1r_1 = v_2r_2$

Answer 1

Answer: (A), (D)

A and D

Answer 2

For a fluid in curvilinear motion, the radial pressure gradient is given by $\frac{dp}{dr} = -\rho \frac{v^2}{r}$. Since $r_2 > r_1$ and pressure decreases towards the center of curvature, $p_1 < p_2$, making option A correct. Streamline spacing indicates velocity; closer streamlines mean higher velocity. As streamlines are denser at $r_1$, $v_1 > v_2$, making option B incorrect. For irrotational flow, $v(r) = C/r$, implying $v_1r_1 = v_2r_2$, making option D correct. Option C is incorrect because $\frac{v_1^2}{r_1} = \frac{C^2}{r_1^3}$ and $\frac{v_2^2}{r_2} = \frac{C^2}{r_2^3}$, and since $r_1 < r_2$, $\frac{v_1^2}{r_1} > \frac{v_2^2}{r_2}$.