Question

A force of 80 N acts on the handle of the paper cutter at A. Determine the moment created by this force about the hinge at O, if $\theta$=60°. At what angle $\theta$ should the force be applied so that the moment it creates about point O is maximum (clockwise)? What is this maximum moment?

Answer 1

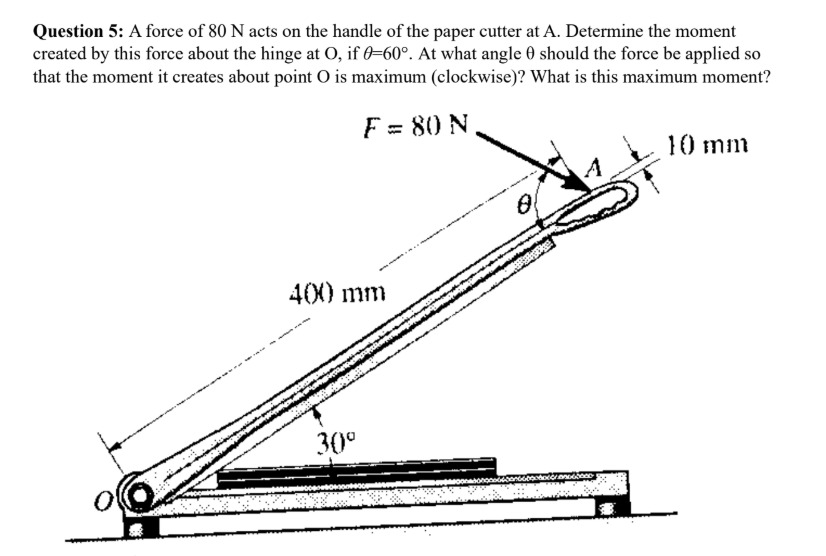
The moment created by the force about the hinge at O, if $\theta=60^\circ$, is $28.4 \, \text{N m}$ (clockwise). The force should be applied at an angle $\theta = 90^\circ$ to the handle so that the moment it creates about point O is maximum. This maximum moment is $32.8 \, \text{N m}$ (clockwise).

Answer 2

1. Calculate Lever Arm: The total distance from the hinge (O) to the point of force application (A) is the sum of the two given lengths: $400 \, \text{mm} + 10 \, \text{mm} = 410 \, \text{mm} = 0.41 \, \text{m}$. This is the lever arm ($r$).

2. Moment at $\theta = 60^\circ$: Use the formula for torque $\tau = r F \sin(\theta)$. Substitute $r = 0.41 \, \text{m}$, $F = 80 \, \text{N}$, and $\theta = 60^\circ$. Calculate the value.

3. Maximum Moment Condition: The moment is maximized when $\sin(\theta)$ is at its maximum value, which is $1$. This occurs when $\theta = 90^\circ$, meaning the force is applied perpendicular to the lever arm.

4. Calculate Maximum Moment: Substitute $r = 0.41 \, \text{m}$, $F = 80 \, \text{N}$, and $\theta = 90^\circ$ (so $\sin(\theta) = 1$) into the torque formula to find the maximum moment.