Question

Let x = 1111 .... 1 (40 digits), y = 222 ...2 (20 digits) and z = 3333....3 (20 digits), then the value of $\frac{x-z^2}{y}$ is

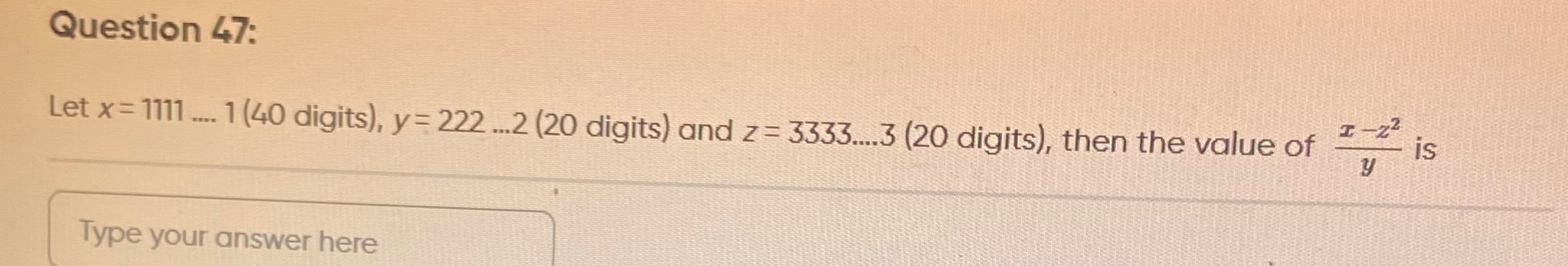
Answer 1

1

Answer 2

Here's how to solve the problem:

1. Represent the numbers algebraically:

   • A repunit with $n$ digits is $\frac{10^n - 1}{9}$.
   • Thus, $$x = \frac{10^{40} - 1}{9}, \quad y = 2 \times \frac{10^{20} - 1}{9}, \quad z = 3 \times \frac{10^{20} - 1}{9}.$$

2. Compute $z^2$:

   $$z = \frac{3(10^{20}-1)}{9} = \frac{10^{20} - 1}{3} \quad \Longrightarrow \quad z^2 = \frac{(10^{20}-1)^2}{9}.$$

3. Evaluate the expression:

   $$\frac{x - z^2}{y} = \frac{\frac{10^{40} - 1}{9} - \frac{(10^{20}-1)^2}{9}}{2\frac{10^{20}-1}{9}} = \frac{(10^{40} - 1) - (10^{20}-1)^2}{2(10^{20}-1)}.$$

4. Simplify: Notice that:

   $$(10^{20}-1)^2 = 10^{40} - 2\cdot10^{20} + 1.$$

   Then, the numerator becomes:

   $$(10^{40} - 1) - (10^{40} - 2\cdot10^{20} + 1) = 2\cdot10^{20} - 2 = 2(10^{20}-1).$$

5. Final Calculation:

   $$\frac{x - z^2}{y} = \frac{2(10^{20}-1)}{2(10^{20}-1)} = 1.$$