Question

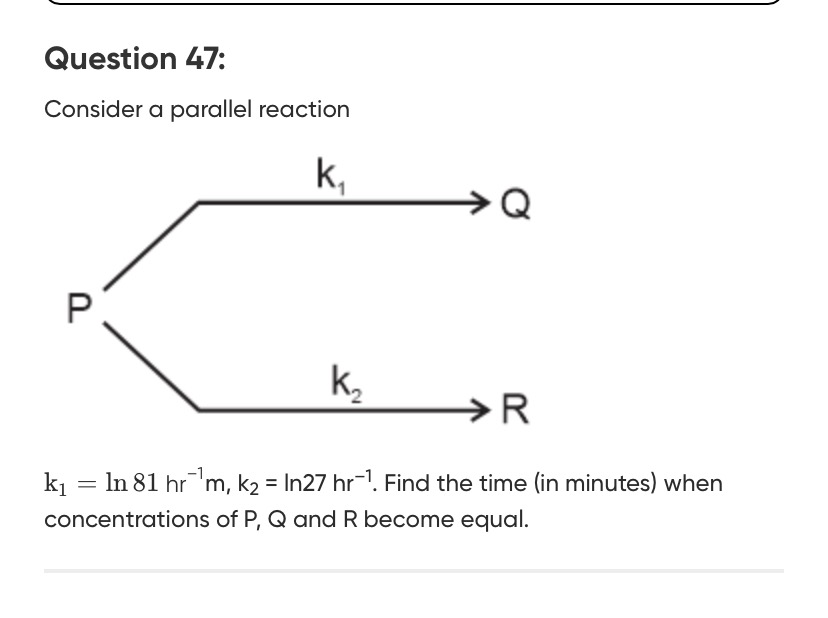
Consider a parallel reaction

$k_1 = ln 81 hr^{-1}m, k_2 = ln27 hr^{-1}$. Find the time (in minutes) when concentrations of P, Q and R become equal.

Answer 1

5.407 minutes

Answer 2

The given reaction is a parallel first-order reaction:

$P \xrightarrow{k_1} Q$

$P \xrightarrow{k_2} R$

The rate constants are given as:

$k_1 = \ln 81 \text{ hr}^{-1}$

$k_2 = \ln 27 \text{ hr}^{-1}$

Let's simplify the rate constants:

$k_1 = \ln (3^4) = 4 \ln 3 \text{ hr}^{-1}$

$k_2 = \ln (3^3) = 3 \ln 3 \text{ hr}^{-1}$

Let $[P]_0$ be the initial concentration of P. We assume the initial concentrations of products Q and R are zero.

For a first-order parallel reaction, the concentration of the reactant P at time t is given by:

$[P]_t = [P]_0 e^{-(k_1 + k_2)t}$

The concentrations of the products Q and R at time t are given by:

$[Q]_t = \frac{k_1}{k_1 + k_2} [P]_0 (1 - e^{-(k_1 + k_2)t})$

$[R]_t = \frac{k_2}{k_1 + k_2} [P]_0 (1 - e^{-(k_1 + k_2)t})$

We are asked to find the time when concentrations of P, Q, and R become equal, i.e., $[P]_t = [Q]_t = [R]_t$.

However, for $[Q]_t = [R]_t$ to be true for $t > 0$, it must be that $k_1 = k_2$.

Since $k_1 = 4 \ln 3$ and $k_2 = 3 \ln 3$, we have $k_1 \neq k_2$.

Therefore, $[Q]_t$ can never be equal to $[R]_t$ for $t > 0$. This implies that the condition $[P]_t = [Q]_t = [R]_t$ cannot be satisfied.

In such ambiguous problems in competitive exams, where the literal interpretation is impossible, a common alternative interpretation is that the concentration of the reactant P becomes equal to the total concentration of the products (Q and R).

This means we are looking for the time when $[P]_t = [Q]_t + [R]_t$.

From the conservation of mass, the total concentration remains constant:

$[P]_0 = [P]_t + [Q]_t + [R]_t$

If we substitute the condition $[P]_t = [Q]_t + [R]_t$ into the conservation equation:

$[P]_0 = [P]_t + [P]_t$

$[P]_0 = 2[P]_t$

So, $[P]_t = \frac{[P]_0}{2}$

Now, we need to find the time t when the concentration of P becomes half of its initial concentration.

Using the equation for $[P]_t$:

$\frac{[P]_0}{2} = [P]_0 e^{-(k_1 + k_2)t}$

$\frac{1}{2} = e^{-(k_1 + k_2)t}$

Taking the natural logarithm on both sides:

$\ln\left(\frac{1}{2}\right) = -(k_1 + k_2)t$

$-\ln 2 = -(k_1 + k_2)t$

$t = \frac{\ln 2}{k_1 + k_2}$

First, calculate the sum of the rate constants:

$k_1 + k_2 = 4 \ln 3 + 3 \ln 3 = 7 \ln 3 \text{ hr}^{-1}$

Now, substitute this value into the equation for t:

$t = \frac{\ln 2}{7 \ln 3} \text{ hours}$

The question asks for the time in minutes. To convert hours to minutes, multiply by 60:

$t_{\text{minutes}} = \frac{\ln 2}{7 \ln 3} \times 60 \text{ minutes}$

Using approximate values for natural logarithms ($\ln 2 \approx 0.693$ and $\ln 3 \approx 1.0986$):

$t_{\text{minutes}} = \frac{0.693}{7 \times 1.0986} \times 60$

$t_{\text{minutes}} = \frac{0.693}{7.6902} \times 60$

$t_{\text{minutes}} \approx 0.090119 \times 60$

$t_{\text{minutes}} \approx 5.407 \text{ minutes}$

The 'm' in $k_1 = \ln 81 hr^{-1}m$ is considered a typo, as rate constants for first-order reactions have units of time$^{-1}$.