Question

Consider the vectors $\vec{a}=\hat{i}+2\hat{j}+4\hat{k}$, $\vec{b}=2\hat{i}+\hat{j}+3\hat{k}$ and $\vec{c}=2\hat{i}+5\hat{j}+\hat{k}$ . Let the vectors $\vec{l}=\sin\theta\vec{a}+\cos\theta\vec{b}-\vec{c}$, $\vec{m}=-\vec{a}+\sin\theta\vec{b}+\cos\theta\vec{c}$ and $\vec{n}=\cos\theta\vec{a}-\vec{b}+\sin\theta\vec{c}$, $\theta \in R$, are three coplanar vectors, then the value of $|\sin\theta-\cos\theta|$ is

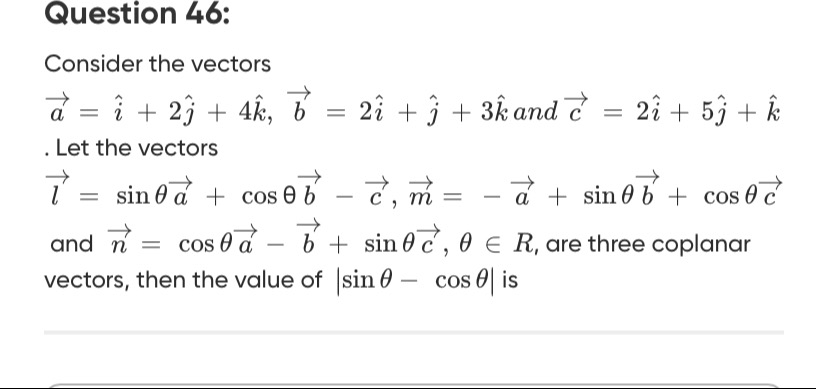
Answer 1

1

Answer 2

Three vectors $\vec{l}$, $\vec{m}$, and $\vec{n}$ are coplanar if their scalar triple product $[\vec{l}, \vec{m}, \vec{n}]$ is zero. The scalar triple product is the determinant of the matrix formed by the coefficients of $\vec{a}$, $\vec{b}$, and $\vec{c}$ in each vector.

The determinant of the coefficient matrix is:

$$\begin{vmatrix} \sin\theta & \cos\theta & -1 \\ -1 & \sin\theta & \cos\theta \\ \cos\theta & -1 & \sin\theta \end{vmatrix} = 0$$

Expanding the determinant: $\sin\theta(\sin^2\theta - (-\cos\theta)) - \cos\theta(-\sin\theta - \cos^2\theta) + (-1)(1 - \sin\theta\cos\theta) = 0$ $\sin^3\theta + \sin\theta\cos\theta + \sin\theta\cos\theta + \cos^3\theta - 1 + \sin\theta\cos\theta = 0$ $\sin^3\theta + \cos^3\theta + 3\sin\theta\cos\theta - 1 = 0$

Let $S = \sin\theta + \cos\theta$. We know that $\sin^2\theta + \cos^2\theta = 1$. $(\sin\theta + \cos\theta)^2 = \sin^2\theta + \cos^2\theta + 2\sin\theta\cos\theta$ $S^2 = 1 + 2\sin\theta\cos\theta \implies \sin\theta\cos\theta = \frac{S^2-1}{2}$.

Using the identity $\sin^3\theta + \cos^3\theta = (\sin\theta + \cos\theta)(\sin^2\theta - \sin\theta\cos\theta + \cos^2\theta) = S(1 - \sin\theta\cos\theta)$: $S(1 - \frac{S^2-1}{2}) + 3(\frac{S^2-1}{2}) - 1 = 0$ $S(\frac{2 - S^2 + 1}{2}) + \frac{3S^2-3}{2} - 1 = 0$ $\frac{S(3-S^2)}{2} + \frac{3S^2-3}{2} - \frac{2}{2} = 0$ $3S - S^3 + 3S^2 - 3 - 2 = 0$ $-S^3 + 3S^2 + 3S - 5 = 0$ $S^3 - 3S^2 - 3S + 5 = 0$

Factoring the cubic equation, we find $S=1$ is a root: $(S-1)(S^2 - 2S - 5) = 0$ The roots are $S=1$ and $S = \frac{2 \pm \sqrt{4 - 4(1)(-5)}}{2} = \frac{2 \pm \sqrt{24}}{2} = 1 \pm \sqrt{6}$.

The range of $S = \sin\theta + \cos\theta = \sqrt{2}\sin(\theta + \frac{\pi}{4})$ is $[-\sqrt{2}, \sqrt{2}]$. $1+\sqrt{6} \approx 1+2.45 = 3.45$, which is outside $[-\sqrt{2}, \sqrt{2}]$. $1-\sqrt{6} \approx 1-2.45 = -1.45$, which is also outside $[-\sqrt{2}, \sqrt{2}]$ (since $-\sqrt{2} \approx -1.414$). Thus, the only valid value is $S = \sin\theta + \cos\theta = 1$.

We need to find $|\sin\theta - \cos\theta|$. Let $D = \sin\theta - \cos\theta$. $D^2 = (\sin\theta - \cos\theta)^2 = \sin^2\theta + \cos^2\theta - 2\sin\theta\cos\theta = 1 - 2\sin\theta\cos\theta$. From $S=1$, we have $1 = \sin\theta + \cos\theta$. Squaring both sides: $1^2 = (\sin\theta + \cos\theta)^2 = 1 + 2\sin\theta\cos\theta$. So, $1 = 1 + 2\sin\theta\cos\theta \implies 2\sin\theta\cos\theta = 0$.

Substituting this into the expression for $D^2$: $D^2 = 1 - 0 = 1$. $|D| = |\sin\theta - \cos\theta| = \sqrt{1} = 1$.