Question

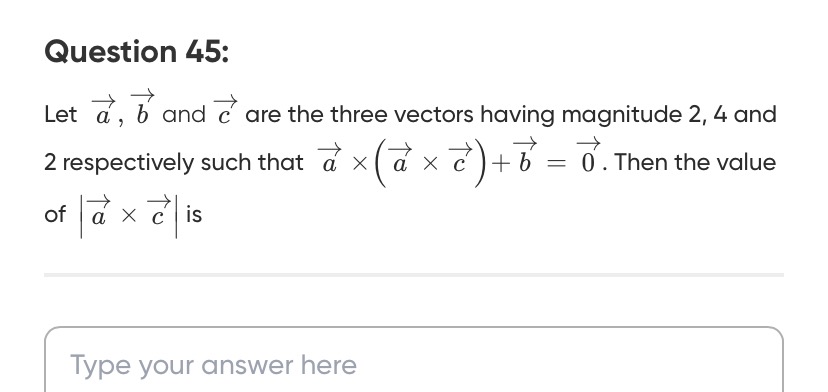
Let $\overrightarrow{a}$, $\overrightarrow{b}$ and $\overrightarrow{c}$ are the three vectors having magnitude 2, 4 and 2 respectively such that $\overrightarrow{a} \times (\overrightarrow{a} \times \overrightarrow{c}) + \overrightarrow{b} = \overrightarrow{0}$. Then the value of $|\overrightarrow{a} \times \overrightarrow{c}|$ is

Answer 1

2

Answer 2

The given vector equation is $\overrightarrow{a} \times (\overrightarrow{a} \times \overrightarrow{c}) + \overrightarrow{b} = \overrightarrow{0}$. This can be rewritten as $\overrightarrow{a} \times (\overrightarrow{a} \times \overrightarrow{c}) = -\overrightarrow{b}$.

Let $\overrightarrow{X} = \overrightarrow{a} \times \overrightarrow{c}$. The equation becomes $\overrightarrow{a} \times \overrightarrow{X} = -\overrightarrow{b}$.

By the definition of the cross product, the vector $\overrightarrow{a} \times \overrightarrow{X}$ is perpendicular to $\overrightarrow{a}$. Since $\overrightarrow{a} \times \overrightarrow{X} = -\overrightarrow{b}$, it implies that $-\overrightarrow{b}$ is perpendicular to $\overrightarrow{a}$. Consequently, $\overrightarrow{b}$ is perpendicular to $\overrightarrow{a}$.

Now, we take the magnitude of both sides of the equation $\overrightarrow{a} \times \overrightarrow{X} = -\overrightarrow{b}$: $|\overrightarrow{a} \times \overrightarrow{X}| = |-\overrightarrow{b}|$ $|\overrightarrow{a} \times \overrightarrow{X}| = |\overrightarrow{b}|$

The magnitude of the cross product $\overrightarrow{a} \times \overrightarrow{X}$ is given by $|\overrightarrow{a}| |\overrightarrow{X}| \sin \phi$, where $\phi$ is the angle between $\overrightarrow{a}$ and $\overrightarrow{X}$. Since $\overrightarrow{a} \times \overrightarrow{X}$ is perpendicular to $\overrightarrow{a}$, the angle $\phi$ must be $90^\circ$ (or $270^\circ$). In either case, $|\sin \phi| = 1$. Therefore, $|\overrightarrow{a} \times \overrightarrow{X}| = |\overrightarrow{a}| |\overrightarrow{X}|$.

Substituting this back into the magnitude equation: $|\overrightarrow{a}| |\overrightarrow{X}| = |\overrightarrow{b}|$

Now, substitute $\overrightarrow{X} = \overrightarrow{a} \times \overrightarrow{c}$: $|\overrightarrow{a}| |\overrightarrow{a} \times \overrightarrow{c}| = |\overrightarrow{b}|$

We are given the magnitudes $|\overrightarrow{a}| = 2$ and $|\overrightarrow{b}| = 4$. $2 |\overrightarrow{a} \times \overrightarrow{c}| = 4$

Solving for $|\overrightarrow{a} \times \overrightarrow{c}|$: $|\overrightarrow{a} \times \overrightarrow{c}| = \frac{4}{2}$ $|\overrightarrow{a} \times \overrightarrow{c}| = 2$