Question

Two blocks each of mass 'm' are connected by an ideal spring of spring constant 'K'. They are given velocities as shown in figure. Find the maximum elongation in spring during the subsequent motion.

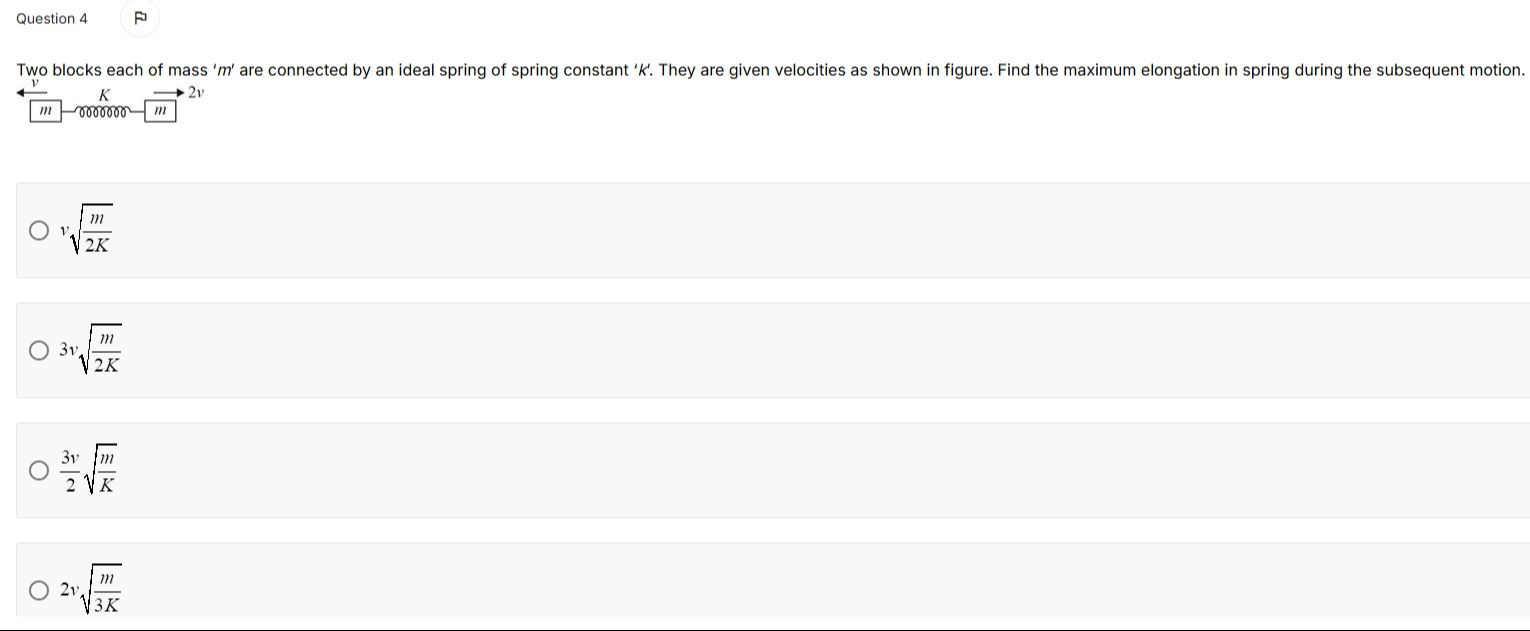
• A. $v \sqrt{\frac{m}{2K}}$
• B. $3v \sqrt{\frac{m}{2K}}$
• C. $\frac{3v}{2} \sqrt{\frac{m}{K}}$
• D. $2v \sqrt{\frac{m}{3K}}$

Answer 1

Answer: (B)

$3v\sqrt{\frac{m}{2K}}$

Answer 2

Let the velocities be taken with the positive sign to the right. Then:

• Left mass: $v_1 = -v$
• Right mass: $v_2 = 2v$

The center-of-mass velocity is:

$$v_{\text{cm}} = \frac{v_1 + v_2}{2} = \frac{-v + 2v}{2} = \frac{v}{2}.$$

Relative velocity (difference) is:

$$v_{\text{rel}} = v_2 - v_1 = 2v - (-v) = 3v.$$

In the center-of-mass frame, the effective initial relative speed is $3v$. For two masses $m$, the reduced mass is:

$$\mu = \frac{m\cdot m}{m+m} = \frac{m}{2}.$$

The initial relative kinetic energy is:

$$KE_{\text{rel}} = \frac{1}{2} \mu (3v)^2 = \frac{1}{2} \cdot \frac{m}{2} \cdot 9v^2 = \frac{9mv^2}{4}.$$

At maximum spring elongation, the entire relative kinetic energy is converted into spring potential energy:

$$\frac{1}{2}K x^2 = \frac{9mv^2}{4}.$$

Solving for $x$:

$$x^2 = \frac{9mv^2}{2K} \quad \Longrightarrow \quad x = 3v \sqrt{\frac{m}{2K}}.$$