Question

The altitude through A of $\triangle ABC$ meets BC at D and the circumscribed circle at E. If $D = (2,3), E = (5,5)$, the ordinate of the orthocenter being a natural number. If the probability that the orthocenter lies on the lines $y = 1; y = 2; y = 3,...... y = 10$ is $\frac{m}{n}$, where $m$ and $n$ are relative primes, the value of $m + n$ is ____.

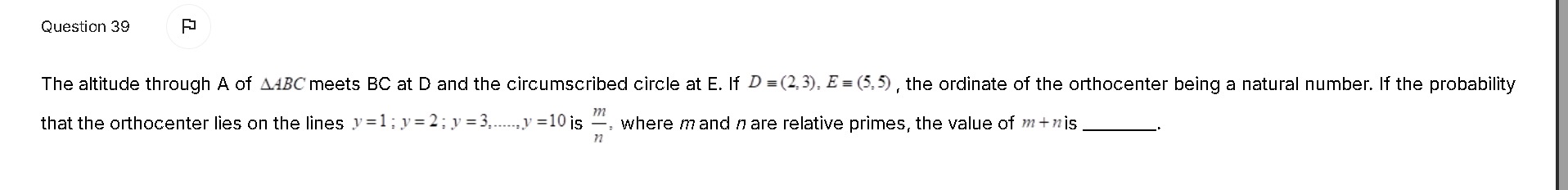
Answer 1

11

Answer 2

1. Use the fact that the foot D of the A–altitude is the midpoint of A and its reflection A′ in BC, and that A′ is the second intersection of the A–altitude with the circumcircle (i.e. E). So,

   $A = 2D – E = 2 \cdot (2,3) – (5,5) = (–1,1)$.

2. The triangle turns out to be right–angled at A (since AB ⟂ AC), so the orthocenter H = A = (–1,1), giving the y–coordinate 1.

3. Among the lines $y = 1,2,…,10$ only $y = 1$ is hit → probability = 1/10, and $m+n = 1+10 = 11$.