Question

$\frac{1}{sin 2^{\circ}} + \frac{1}{sin 4^{\circ}} + \frac{1}{sin 8^{\circ}} + \frac{1}{sin 16^{\circ}} + \frac{1}{sin 32^{\circ}} + \frac{1}{sin 64^{\circ}}$ is equal to

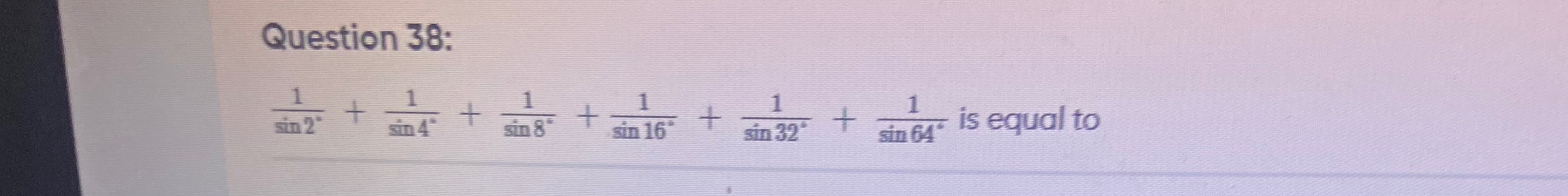
Answer 1

$\cot1^\circ-\cot64^\circ$

Answer 2

We use the identity

$$\csc\theta = \cot\frac{\theta}{2} - \cot\theta.$$

Apply this to each term:

$$\begin{aligned} \frac{1}{\sin 2^\circ} &= \csc2^\circ = \cot1^\circ - \cot2^\circ,\\[1mm] \frac{1}{\sin 4^\circ} &= \csc4^\circ = \cot2^\circ - \cot4^\circ,\\[1mm] \frac{1}{\sin 8^\circ} &= \csc8^\circ = \cot4^\circ - \cot8^\circ,\\[1mm] \frac{1}{\sin 16^\circ} &= \csc16^\circ = \cot8^\circ - \cot16^\circ,\\[1mm] \frac{1}{\sin 32^\circ} &= \csc32^\circ = \cot16^\circ - \cot32^\circ,\\[1mm] \frac{1}{\sin 64^\circ} &= \csc64^\circ = \cot32^\circ - \cot64^\circ. \end{aligned}$$

Adding all these we see the telescoping cancellation:

$$\begin{aligned} S &= (\cot1^\circ-\cot2^\circ) + (\cot2^\circ-\cot4^\circ) + (\cot4^\circ-\cot8^\circ) \\ &\quad + (\cot8^\circ-\cot16^\circ) + (\cot16^\circ-\cot32^\circ) + (\cot32^\circ-\cot64^\circ) \\ &= \cot1^\circ - \cot64^\circ. \end{aligned}$$

Explanation (minimal):

Using $\csc\theta=\cot\frac{\theta}{2}-\cot\theta$, write each term and add them to get a telescoping sum which reduces to $\cot1^\circ-\cot64^\circ$.