Question

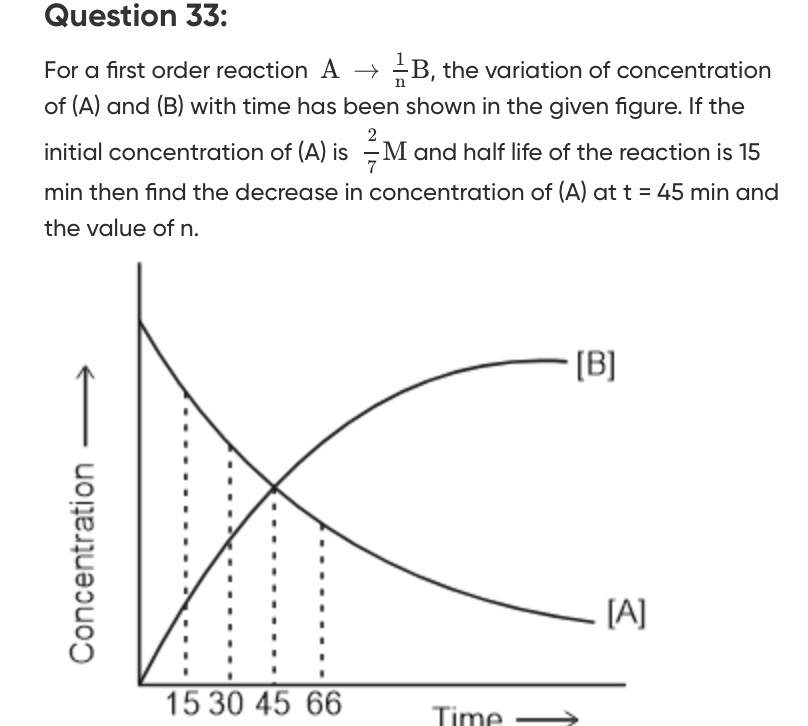
For a first order reaction $A \longrightarrow \frac{1}{n}B$, the variation of concentration of (A) and (B) with time has been shown in the given figure. If the initial concentration of (A) is $\frac{2}{7}M$ and half life of the reaction is 15 min then find the decrease in concentration of (A) at t = 45 min and the value of n.

Answer 1

Decrease in concentration of (A) at t = 45 min is $\frac{1}{4}M$ and the value of n is 7.

Answer 2

The problem involves a first-order reaction and requires calculating the decrease in concentration of a reactant and determining a stoichiometric coefficient using half-life and graphical information.

1. Calculate the decrease in concentration of (A) at t = 45 min: For a first-order reaction, the half-life ($t_{1/2}$) is constant. Given $t_{1/2} = 15$ min. The time elapsed is $t = 45$ min. The number of half-lives that have passed is $m = \frac{t}{t_{1/2}} = \frac{45 \text{ min}}{15 \text{ min}} = 3$.

For a first-order reaction, the concentration of reactant remaining after 'm' half-lives is given by: $[A]_t = \frac{[A]_0}{2^m}$ Given initial concentration $[A]_0 = \frac{2}{7} M$. At $t = 45$ min (after 3 half-lives): $[A]_{45} = \frac{[A]_0}{2^3} = \frac{[A]_0}{8}$ $[A]_{45} = \frac{1}{8} \times \frac{2}{7} M = \frac{1}{4} \times \frac{1}{7} M = \frac{1}{28} M$.

The decrease in concentration of (A) is the initial concentration minus the concentration at time t: Decrease in $[A] = [A]_0 - [A]_{45}$ Decrease in $[A] = \frac{2}{7} M - \frac{1}{28} M$ To subtract, find a common denominator (28): Decrease in $[A] = \frac{2 \times 4}{7 \times 4} M - \frac{1}{28} M = \frac{8}{28} M - \frac{1}{28} M = \frac{7}{28} M = \frac{1}{4} M$.

2. Find the value of n: The reaction is $A \longrightarrow \frac{1}{n}B$. From the graph, at $t = 45$ min, the concentration of A and B are equal (the curves intersect). So, $[B]_{45} = [A]_{45} = \frac{1}{28} M$.

Let $x$ be the amount of A reacted at $t = 45$ min. $x = [A]_0 - [A]_{45} = \frac{1}{4} M$.

According to the stoichiometry of the reaction $A \longrightarrow \frac{1}{n}B$: If 1 mole of A reacts, $\frac{1}{n}$ moles of B are formed. If $x$ moles of A react, then $\frac{1}{n}x$ moles of B are formed. So, $[B]_{45} = \frac{1}{n}x$.

Substitute the known values: $\frac{1}{28} M = \frac{1}{n} \times \frac{1}{4} M$ $\frac{1}{28} = \frac{1}{4n}$ Cross-multiply: $4n = 28$ $n = \frac{28}{4}$ $n = 7$.