Question

Let $P = \lim_{k \to \infty} \left[ \frac{e^{\frac{1}{k}}}{k^2} + \frac{2(e^{\frac{1}{k}})^2}{k^2} + \frac{3(e^{\frac{1}{k}})^3}{k^2} + ... + \frac{k(e^{\frac{1}{k}})^k}{k^2} \right]$. Then, the value of $P^{P^{P... (2016) times}}$ is

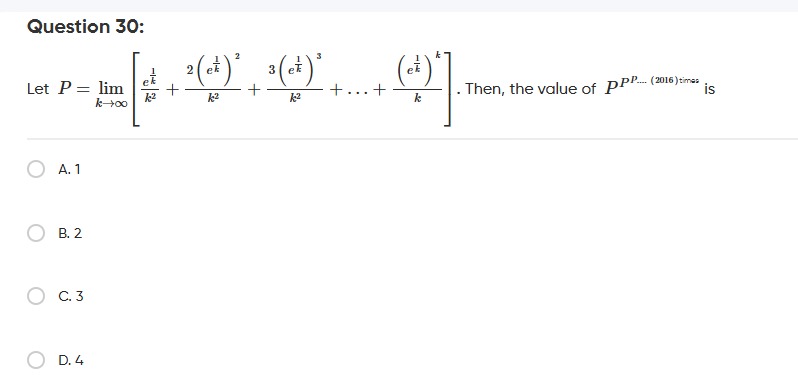
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (A)

1

Answer 2

The limit can be rewritten as $P = \lim_{k \to \infty} \frac{1}{k^2} \sum_{n=1}^{k} n \left(e^{\frac{1}{k}}\right)^n$. This is a Riemann sum for the integral $\int_{0}^{1} x e^x dx$. Evaluating the integral using integration by parts: $\int_{0}^{1} x e^x dx = [x e^x]_{0}^{1} - \int_{0}^{1} e^x dx = (1 \cdot e^1 - 0) - [e^x]_{0}^{1} = e - (e^1 - e^0) = e - (e - 1) = 1$. Thus, $P=1$. The expression $P^{P^{P... (2016) times}}$ becomes $1^{1^{1^{... (2016) times}}}$, which is equal to 1.