Solveeit Logo
Login

Question

Question: Let $\int \frac{dz}{(1+z^2)^4}=a\frac{z}{(1+z^2)^3}+b\frac{z}{(1+z^2)^2}+c\frac{z}{(1+z^2)}+ d\tan^{...

Let ∫dz(1+z2)4=az(1+z2)3+bz(1+z2)2+cz(1+z2)+dtan⁡−1x+K\int \frac{dz}{(1+z^2)^4}=a\frac{z}{(1+z^2)^3}+b\frac{z}{(1+z^2)^2}+c\frac{z}{(1+z^2)}+ d\tan^{-1}x+K, where KK is constant of integration. Then which of the following option(s) is/are correct?

A

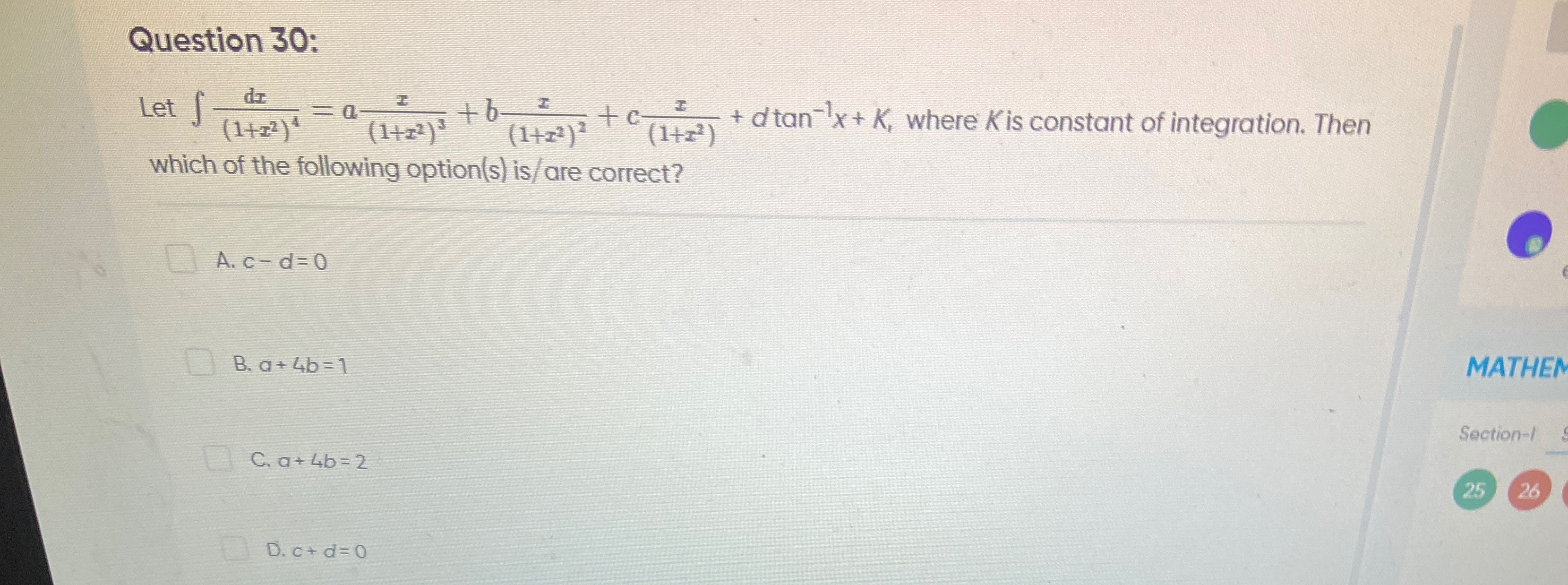
c - d = 0

B

a + 4b = 1

C

a + 4b = 2

D

c + d = 0

Answer

A, B

Explanation

Solution

To solve the integral ∫dz(1+z2)4\int \frac{dz}{(1+z^2)^4}, we can use a reduction formula for integrals of the form In=∫dz(1+z2)nI_n = \int \frac{dz}{(1+z^2)^n}.

The reduction formula is given by: In=z2(n−1)(1+z2)n−1+2n−32(n−1)In−1I_n = \frac{z}{2(n-1)(1+z^2)^{n-1}} + \frac{2n-3}{2(n-1)} I_{n-1} for n≥2n \ge 2.
And I1=∫dz1+z2=tan⁡−1zI_1 = \int \frac{dz}{1+z^2} = \tan^{-1}z.

We need to find I4I_4. We will apply the formula iteratively:

  1. For n=2n=2:
    I2=z2(2−1)(1+z2)2−1+2(2)−32(2−1)I1I_2 = \frac{z}{2(2-1)(1+z^2)^{2-1}} + \frac{2(2)-3}{2(2-1)} I_1
    I2=z2(1)(1+z2)1+12(1)I1I_2 = \frac{z}{2(1)(1+z^2)^1} + \frac{1}{2(1)} I_1
    I2=z2(1+z2)+12tan⁡−1zI_2 = \frac{z}{2(1+z^2)} + \frac{1}{2}\tan^{-1}z

  2. For n=3n=3:
    I3=z2(3−1)(1+z2)3−1+2(3)−32(3−1)I2I_3 = \frac{z}{2(3-1)(1+z^2)^{3-1}} + \frac{2(3)-3}{2(3-1)} I_2
    I3=z4(1+z2)2+34I2I_3 = \frac{z}{4(1+z^2)^2} + \frac{3}{4} I_2
    Substitute I2I_2:
    I3=z4(1+z2)2+34(z2(1+z2)+12tan⁡−1z)I_3 = \frac{z}{4(1+z^2)^2} + \frac{3}{4} \left( \frac{z}{2(1+z^2)} + \frac{1}{2}\tan^{-1}z \right)
    I3=z4(1+z2)2+3z8(1+z2)+38tan⁡−1zI_3 = \frac{z}{4(1+z^2)^2} + \frac{3z}{8(1+z^2)} + \frac{3}{8}\tan^{-1}z

  3. For n=4n=4:
    I4=z2(4−1)(1+z2)4−1+2(4)−32(4−1)I3I_4 = \frac{z}{2(4-1)(1+z^2)^{4-1}} + \frac{2(4)-3}{2(4-1)} I_3
    I4=z6(1+z2)3+56I3I_4 = \frac{z}{6(1+z^2)^3} + \frac{5}{6} I_3
    Substitute I3I_3:
    I4=z6(1+z2)3+56(z4(1+z2)2+3z8(1+z2)+38tan⁡−1z)I_4 = \frac{z}{6(1+z^2)^3} + \frac{5}{6} \left( \frac{z}{4(1+z^2)^2} + \frac{3z}{8(1+z^2)} + \frac{3}{8}\tan^{-1}z \right)
    I4=z6(1+z2)3+5z24(1+z2)2+15z48(1+z2)+1548tan⁡−1zI_4 = \frac{z}{6(1+z^2)^3} + \frac{5z}{24(1+z^2)^2} + \frac{15z}{48(1+z^2)} + \frac{15}{48}\tan^{-1}z
    Simplify the coefficients:
    I4=16z(1+z2)3+524z(1+z2)2+516z(1+z2)+516tan⁡−1z+KI_4 = \frac{1}{6}\frac{z}{(1+z^2)^3} + \frac{5}{24}\frac{z}{(1+z^2)^2} + \frac{5}{16}\frac{z}{(1+z^2)} + \frac{5}{16}\tan^{-1}z + K

Comparing this with the given form:
∫dz(1+z2)4=az(1+z2)3+bz(1+z2)2+cz(1+z2)+dtan⁡−1x+K\int \frac{dz}{(1+z^2)^4}=a\frac{z}{(1+z^2)^3}+b\frac{z}{(1+z^2)^2}+c\frac{z}{(1+z^2)}+ d\tan^{-1}x+K
(Assuming xx in tan⁡−1x\tan^{-1}x is a typo and should be zz)

We identify the coefficients:
a=16a = \frac{1}{6}
b=524b = \frac{5}{24}
c=516c = \frac{5}{16}
d=516d = \frac{5}{16}

Now we check the given options:

A. c - d = 0
c−d=516−516=0c - d = \frac{5}{16} - \frac{5}{16} = 0. This option is correct.

B. a + 4b = 1
a+4b=16+4(524)=16+2024=16+56=66=1a + 4b = \frac{1}{6} + 4 \left(\frac{5}{24}\right) = \frac{1}{6} + \frac{20}{24} = \frac{1}{6} + \frac{5}{6} = \frac{6}{6} = 1. This option is correct.

C. a + 4b = 2
Since option B is correct, this option is incorrect.

D. c + d = 0
c+d=516+516=1016=58≠0c + d = \frac{5}{16} + \frac{5}{16} = \frac{10}{16} = \frac{5}{8} \neq 0. This option is incorrect.

The correct options are A and B.