Question

A particle is moving in front of a thin equi-convex lens of radius of curvature 10 cm and refractive index $\frac{4}{3}$. Figure shows an instant when the particle is making 60° with the principal axis and its image is making 30° with the axis. List-I mentions some quantities at the instant shown and List-II mentions their corresponding values.

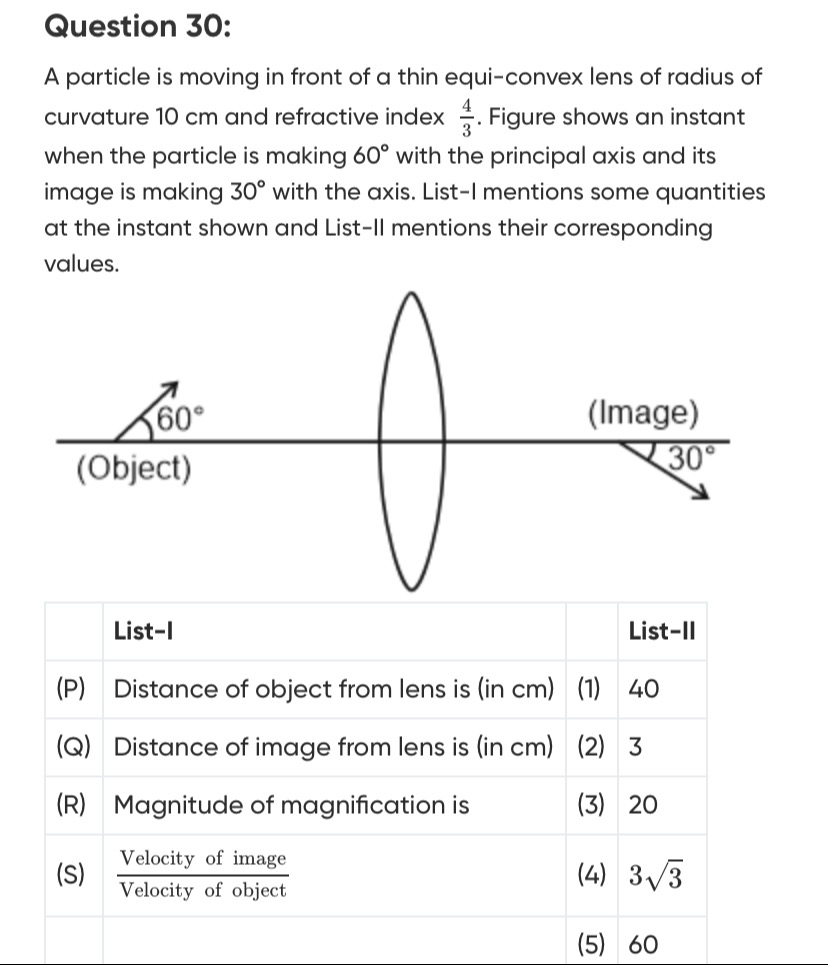
• A. Distance of object from lens is (in cm)
• B. Distance of image from lens is (in cm)
• C. Magnitude of magnification is
• D. $\frac{\text { Velocity of image}}{\text { Velocity of object}}$
• E. 40
• F. 3
• G. 20
• H. $3\sqrt{3}$
• I. 60

Answer 1

P-3, Q-5, R-2, S-4

Answer 2

To solve this problem, we need to calculate the focal length of the lens, then use the relationship between the object and image velocities to find the magnification, and finally use the lens formula to determine object and image distances.

1. Calculate the focal length (f) of the equi-convex lens: Given: Radius of curvature $R = 10$ cm, refractive index $\mu = \frac{4}{3}$. For an equi-convex lens, $R_1 = +R = +10$ cm and $R_2 = -R = -10$ cm. Using the lens maker's formula: $\frac{1}{f} = (\mu - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)$ $\frac{1}{f} = \left(\frac{4}{3} - 1\right) \left( \frac{1}{10} - \frac{1}{-10} \right)$ $\frac{1}{f} = \left(\frac{1}{3}\right) \left( \frac{1}{10} + \frac{1}{10} \right)$ $\frac{1}{f} = \left(\frac{1}{3}\right) \left( \frac{2}{10} \right) = \frac{1}{15}$ So, the focal length of the lens is $f = 15$ cm.

2. Determine the transverse magnification ($m_T$): Let $v_O$ be the speed of the object and $v_I$ be the speed of the image. The object's velocity components are: $v_{Ox} = v_O \cos 60^\circ$ (longitudinal component) $v_{Oy} = v_O \sin 60^\circ$ (transverse component)

The image's velocity components are: $v_{Ix} = v_I \cos 30^\circ$ (longitudinal component) $v_{Iy} = v_I \sin 30^\circ$ (transverse component)

For a lens, the relationship between longitudinal velocity components is $v_{Ix} = m_T^2 v_{Ox}$ and for transverse velocity components is $v_{Iy} = m_T v_{Oy}$. However, we need to be careful with signs. A real image formed by a convex lens is inverted, so $m_T$ is negative. Let's consider the directions from the diagram. The object is approaching the lens (negative x-direction for $v_{Ox}$) and moving upwards (positive y-direction for $v_{Oy}$). The image is moving away from the lens (positive x-direction for $v_{Ix}$) and downwards (negative y-direction for $v_{Iy}$).

So, $v_{Ox} = -v_O \cos 60^\circ$ and $v_{Oy} = v_O \sin 60^\circ$. And $v_{Ix} = v_I \cos 30^\circ$ and $v_{Iy} = -v_I \sin 30^\circ$.

Using the relations: (1) $v_{Iy} = m_T v_{Oy} \implies -v_I \sin 30^\circ = m_T (v_O \sin 60^\circ)$ (2) $v_{Ix} = m_T^2 v_{Ox} \implies v_I \cos 30^\circ = m_T^2 (-v_O \cos 60^\circ)$

From (1): $\frac{v_I}{v_O} = -m_T \frac{\sin 60^\circ}{\sin 30^\circ} = -m_T \frac{\sqrt{3}/2}{1/2} = -m_T \sqrt{3}$ From (2): $\frac{v_I}{v_O} = -m_T^2 \frac{\cos 60^\circ}{\cos 30^\circ} = -m_T^2 \frac{1/2}{\sqrt{3}/2} = -\frac{m_T^2}{\sqrt{3}}$

Equating the two expressions for $\frac{v_I}{v_O}$: $-m_T \sqrt{3} = -\frac{m_T^2}{\sqrt{3}}$ Since $m_T \neq 0$, we can divide by $-m_T$: $\sqrt{3} = \frac{m_T}{\sqrt{3}}$ $m_T = 3$ This result for $m_T$ is positive, which implies an erect image. However, for a real image formed by a convex lens, the image is inverted, meaning $m_T$ should be negative. The angular relationship implies the ratio of speeds is positive, but the actual $m_T$ should be negative. The "magnitude of magnification" is asked in (R). So, $|m_T| = 3$. This matches with List-II (2).

3. Calculate object and image distances (u and v): Let $u$ be the object position and $v$ be the image position. By convention, $u$ is negative and $v$ is positive for a real image. The transverse magnification is $m_T = \frac{v}{u}$. Since the image is real and inverted, $m_T = -3$. So, $\frac{v}{u} = -3 \implies v = -3u$.

Using the lens formula: $\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$ Substitute $v = -3u$ and $f = 15$ cm: $\frac{1}{-3u} - \frac{1}{u} = \frac{1}{15}$ $\frac{-1 - 3}{3u} = \frac{1}{15}$ $\frac{-4}{3u} = \frac{1}{15}$ $3u = -4 \times 15$ $3u = -60$ $u = -20 \text{ cm}$ The distance of the object from the lens is $|u| = 20$ cm. This matches with List-II (3).

Now calculate $v$: $v = -3u = -3(-20) = 60 \text{ cm}$ The distance of the image from the lens is $|v| = 60$ cm. This matches with List-II (5).

4. Calculate the ratio of velocities $\frac{\text { Velocity of image}}{\text { Velocity of object}}$: Using the expression derived earlier: $\frac{v_I}{v_O} = -m_T \sqrt{3}$ Substitute $m_T = -3$: $\frac{v_I}{v_O} = -(-3) \sqrt{3} = 3\sqrt{3}$ This matches with List-II (4).

Summary of matches:

• (P) Distance of object from lens is (in cm) $\rightarrow$ 20 (List-II (3))
• (Q) Distance of image from lens is (in cm) $\rightarrow$ 60 (List-II (5))
• (R) Magnitude of magnification is $\rightarrow$ 3 (List-II (2))
• (S) $\frac{\text { Velocity of image}}{\text { Velocity of object}}$ $\rightarrow$ $3\sqrt{3}$ (List-II (4))

The question is a matching type, and all options are uniquely matched.