Question

Find the electron gain enthalpy of iodine with the help of the following data: Heat of formation of NaI = -287.9 kJ/mol Heat of Sublimation of Na = 108.4 kJ/mol Ionisation energy of Na = 106.7 kJ/mol Heat of atomisation of iodine = 495.4 kJ/mol Lattice energy of NaI = -692 kJ/mol

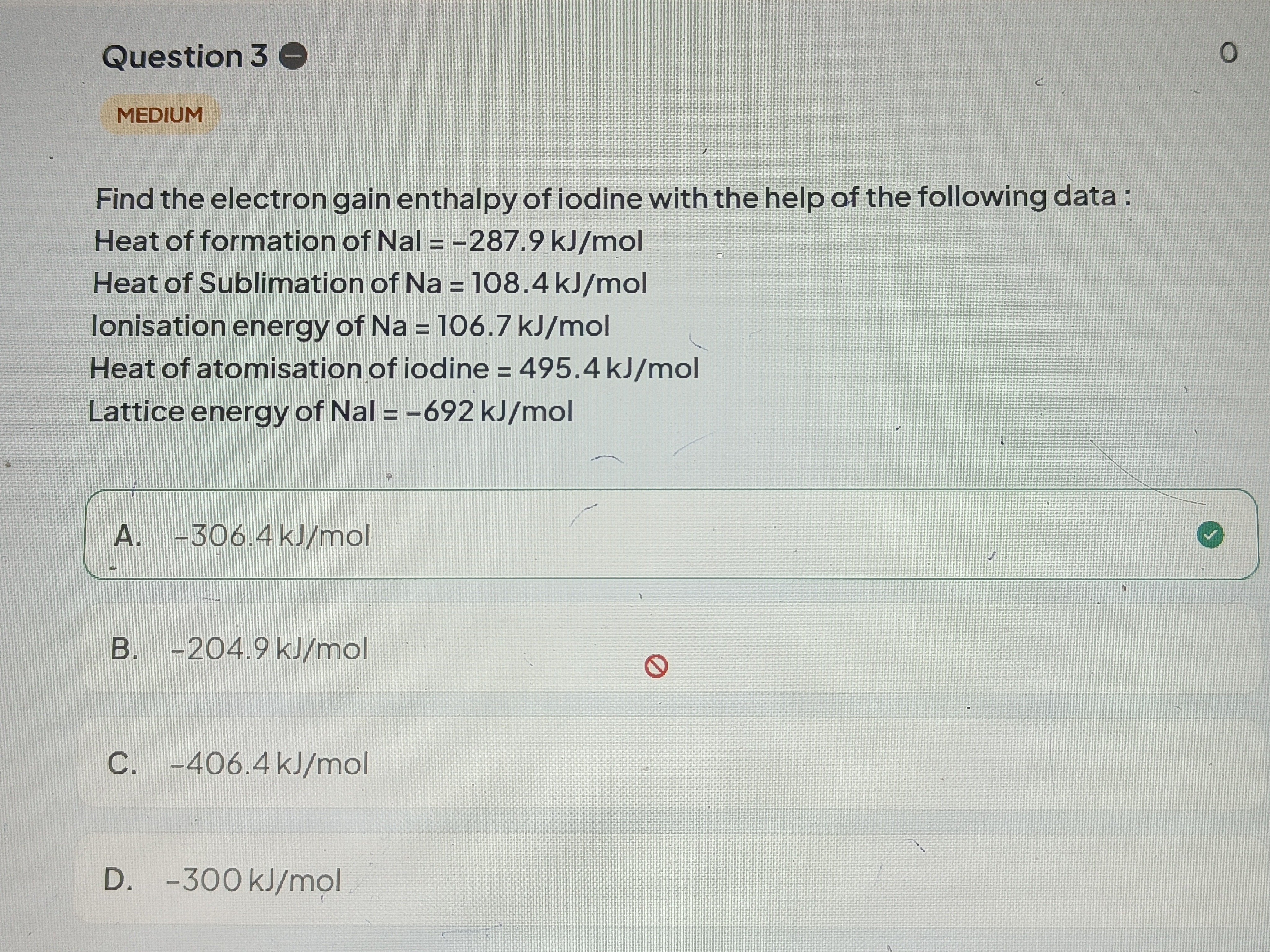
• A. -306.4 kJ/mol
• B. -204.9 kJ/mol
• C. -406.4 kJ/mol
• D. -300 kJ/mol

Answer 1

Answer: (A)

-306.4 kJ/mol

Answer 2

The Born-Haber cycle is used to determine the electron gain enthalpy. The cycle represents the formation of an ionic compound from its constituent elements through a series of steps. The enthalpy change for each step is known, and the overall enthalpy of formation is also known. By applying Hess's Law, the unknown enthalpy change (in this case, electron gain enthalpy) can be calculated.

The steps involved in the Born-Haber cycle for NaI are:

1. Sublimation of Sodium: Na(s) $\to$ Na(g) ; $\Delta H_{sub}$ = 108.4 kJ/mol
2. Ionization of Sodium: Na(g) $\to$ Na⁺(g) + e⁻ ; IE = 106.7 kJ/mol
3. Atomization of Iodine: 1/2 I₂(s) $\to$ I(g) ; $\Delta H_{atom\_I}$ = 495.4 kJ/mol
4. Electron Gain by Iodine: I(g) + e⁻ $\to$ I⁻(g) ; $\Delta H_{eg}$ (Electron Gain Enthalpy of Iodine) = ?
5. Formation of Lattice: Na⁺(g) + I⁻(g) $\to$ NaI(s) ; $\Delta H_{lattice}$ = -692 kJ/mol

The enthalpy of formation ($\Delta H_f^\circ$) of NaI is the sum of the enthalpies of these steps: $\Delta H_f^\circ$ = $\Delta H_{sub}$ + IE + $\Delta H_{atom\_I}$ + $\Delta H_{eg}$ + $\Delta H_{lattice}$

Given values: $\Delta H_f^\circ$ (NaI) = -287.9 kJ/mol $\Delta H_{sub}$ (Na) = 108.4 kJ/mol IE (Na) = 106.7 kJ/mol $\Delta H_{atom\_I}$ (1/2 I₂(s) $\to$ I(g)) = 495.4 kJ/mol $\Delta H_{lattice}$ (NaI) = -692 kJ/mol

Substitute the values into the equation: -287.9 kJ/mol = 108.4 kJ/mol + 106.7 kJ/mol + 495.4 kJ/mol + $\Delta H_{eg}$ + (-692 kJ/mol)

Sum the known enthalpy values: 108.4 + 106.7 + 495.4 - 692 = 710.5 - 692 = 18.5 kJ/mol

The equation becomes: -287.9 kJ/mol = 18.5 kJ/mol + $\Delta H_{eg}$

Solve for $\Delta H_{eg}$: $\Delta H_{eg}$ = -287.9 kJ/mol - 18.5 kJ/mol $\Delta H_{eg}$ = -306.4 kJ/mol